1. 서 론
2. 열화모델
2.1 지반의 강도저하 모델
2.2 지반 강도저하 모델 제안
3. 열화모델을 활용한 지하생활기반시설물 장기거동 예측
3.1 강도정수 열화곡선
3.2 수치해석
3.3 수치해석 해석결과
4. 결 과
1. 서 론
평지가 적은 우리나라 특성상 한정된 지상공간을 대신하여 가용용지 확보 등의 목적으로 지하공간을 활용하고자 다양한 사업을 추진 및 계획 중이다. 그러나 도심지 내 지하 생활기반시설 구축을 위한 지반 굴착에 따른 지반 붕괴 및 주변 구조물의 피해가 증가하고 있다. 이러한 굴착으로 인해 발생된 지반 붕괴 및 구조물의 피해를 저감하기 위해서는 국내실정에 맞는 열화모델 개발이 필요하다.
Nakagawa et al.(2004), Kawata et al.(2005) 그리고 Jiang et al.(2007)은 지하 굴착에 의해 발생한 소성영역이 시간이 지남에 따라 지반이 열화를 수치적으로 산정하기 위해 Sato & Kamemura(1984)가 제안한 파괴시간-응력비의 관계곡선으로부터 구조물의 거동을 분석하였다. Matsunaga(2008)와 Yashiro et al.(2009)는 노후된 지하시설물에서 계측된 내공변위 및 지반조사 자료를 바탕으로 지반의 열화에 따른 전단강도는 Log 함수에 따라 감소하는 식을 제시하였다. Han(2018)은 지반열화로 인해 사면 붕괴가 발생한 셰일층 사면 사례를 수치해석을 하여 지반열화로 인한 안전율 변화를 살펴보았다. 수치해석 결과 사면의 안전율이 3.05와 3.21로 안전했으나, 열화가 진행됨에 따라 안전율이 1.13과 1.00으로 감소하였음을 보고하였다. Kim & Sin(2007)는 열화에 따른 구조체의 장기거동을 예측하고자 수치해석적으로 모델링하기 위한 해석기법을 제안하였다. 이러한 해석기법을 터널 설계상에서의 적용성을 검토하였으며, 열화 조건에서 주변 지반 응력상태에 따라 구조체의 물리적 손상도와 속도가 크게 달라짐을 보고하였다. Lee et al.(2009)는 터널의 열화 원인을 찾고자 1990년대 중반에 시공된 3-arch터널 4개소를 선정하여 열화현상을 조사하였다. 조사 결과 모든 터널에서 중앙 기둥 측의 상하선 아치부에서 유사한 종방향 균열을 확인하였으며, 콘크리트 라이닝의 철근 배근 불량과 굴착 시의 영향으로 인해 터널 열화가 발생함을 보고하였다. Ahn(2022)는 지반 열화로 인해 지하 구조물의 변위 거동이 침목 플로팅 궤도에 미치는 영향을 분석하기 위해 수치해석을 수행하였다. 수치해석 결과 구조물의 융기나 침하 시 뜬 침목이 발생하며, 레일 변위는 구조물의 침하량보다 작은 것으로 나타남을 보고하였다.
따라서 본 연구에서는 지하 구조물의 장기거동 예측을 통해 보수, 보강의 시기를 결정할 수 있도록 열화모델을 제시하였다. 제시한 열화모델을 유한요소 수치해석 프로그램인 ABAQUS를 활용하여 시간경과에 따른 사면의 소성변형률의 변화로 사면의 파괴면과 안전율의 변화를 살펴보았다.
2. 열화모델
2.1 지반의 강도저하 모델
지하 생활기반시설물을 둘러싸고 있는 지반의 대표적인 물성치인 지반반력계수, 강도정수 등은 시간이 흐름에 따라 강도저하를 보인다. 이러한 시간에 따른 강도저하로 인해 지하생활기반시설물 주변의 소성화로 인한 소성압이 증가하게 되고 그 결과 주변지반의 이완영역의 확대로 인해 지하생활기반시설물의 안정성에 영향을 미친다.
이러한 지하생활기반시설물 주변 지반이 열화되는 특성에 대해 많은 선행연구가 수행되었다. Nakagawa et al.(2004), Kawata et al.(2005) 그리고 Jiang et al.(2007)은 지하 굴착에 의해 발생한 소성영역이 시간이 지남에 따라 지반이 열화를 수치적으로 산정하기 위해 Sato & Kamemura(1984)가 제안한 파괴시간-응력비의 관계곡선(Eq. (1))으로부터 구조물의 거동을 분석하였다. 이때 시간의존에 의해 열화되는 물성치는 점착력만을 대상으로 하였다.
여기서, : Mohr-Coulomb의 파괴비(응력계수)
: 강도 저하속도
Matsunaga(2008)와 Yashiro et al.(2009)는 노후된 지하시설물에서 계측된 내공변위 및 지반조사 자료를 바탕으로 지반의 열화에 따른 전단강도는 Log 함수에 따라 감소하는 식을 제시하였다(Eq. (2)).
여기서, : 지반의 초기전단강도
: 계수
: 경과시간
Ladanyi(1974)는 지반의 강도특성은 장기적으로 초기치의 30%까지 감소한다고 보고하였으며, 이를 근거로 Sandrone & Labiouse(2010)은 지반의 강도변화가 쌍곡선법(hyperbolic)을 따르며, 임의 시간에 대한 강도를 Eq. (3)으로 구할 수 있다고 제시하였다.
여기서, : 입력변수 초기치(점착력 및 마찰계수)
: 입력변수의 최종 값(초기치의 30%)
: 일정 값(지반열화의 총 시간)
: 시설물 시공 완료 후 경과시간
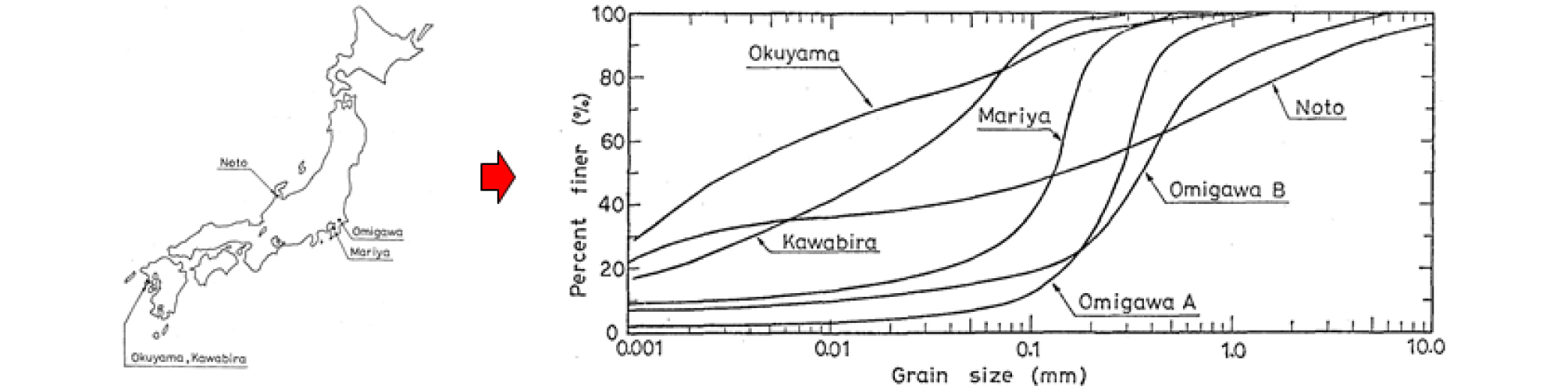
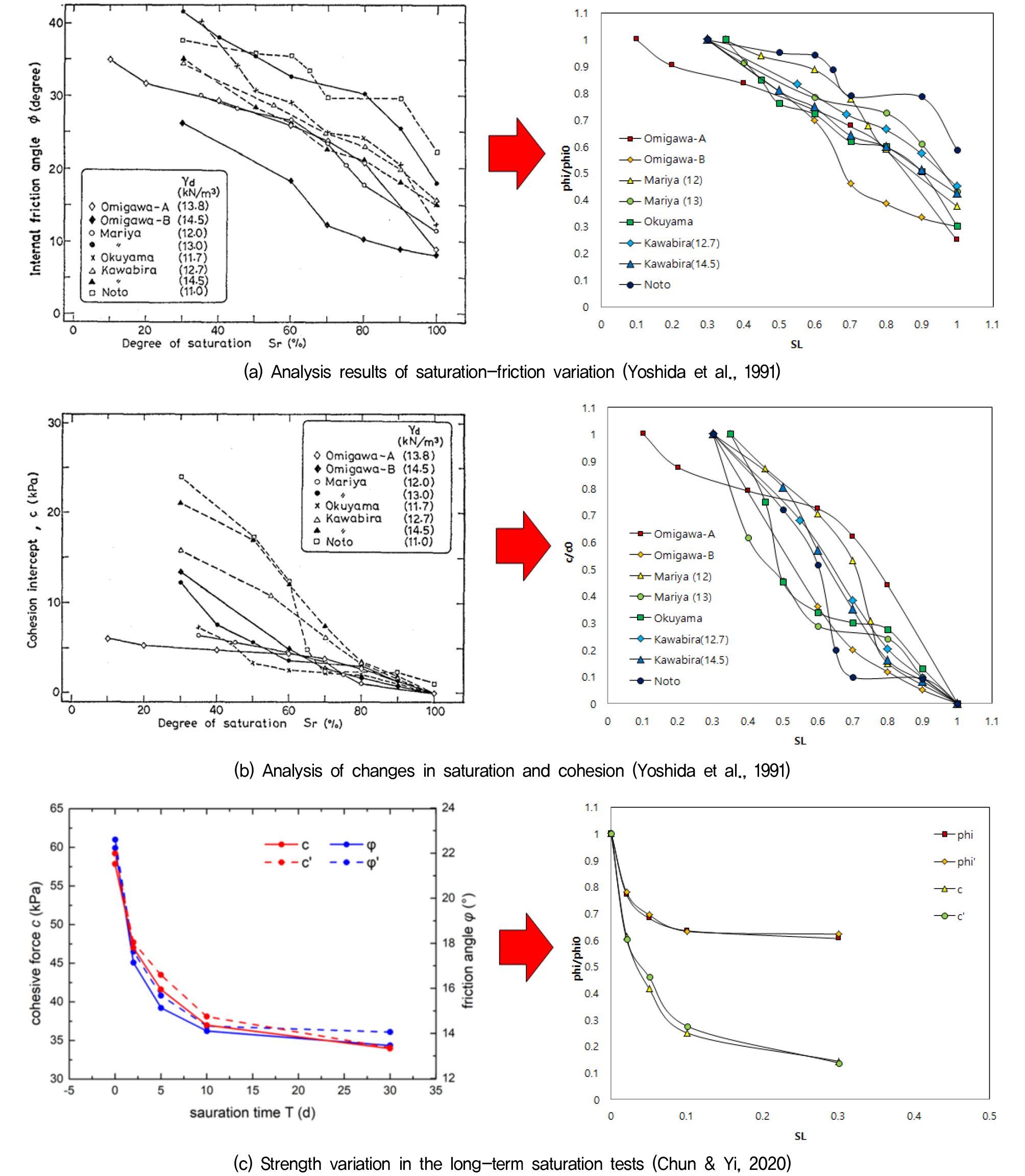
Yoshida et al.(1991)은 지반의 강도특성을 분석하기 위해 일본의 지역 중 경사면이 붕괴된 Noto, Omigawa, Mariya, Okuyama, Kawabira 지역의 시료를 채취하여 분석하였다(Fig. 1).
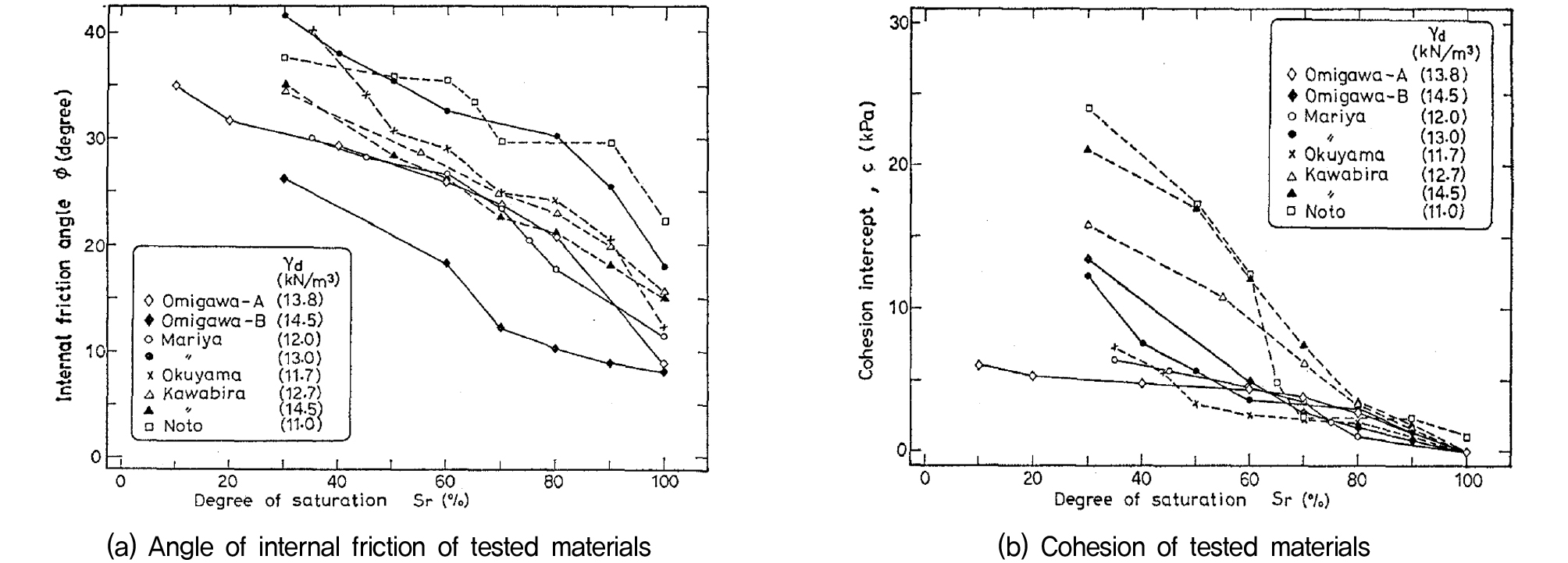
지반의 강도특성을 분석한 결과는 Fig. 2에 나타냈다. Fig. 2(a)는 포화도 변화에 따른 마찰력을 나타낸 그래프로 포화도가 증가함에 따라 지반의 마찰력이 낮아짐을 확인하였다. Fig. 2(b)는 포화도 변화에 따른 점착력을 나타낸 그래프로 포화도가 증가함에 따라 점착력이 낮아짐을 확인하였다.
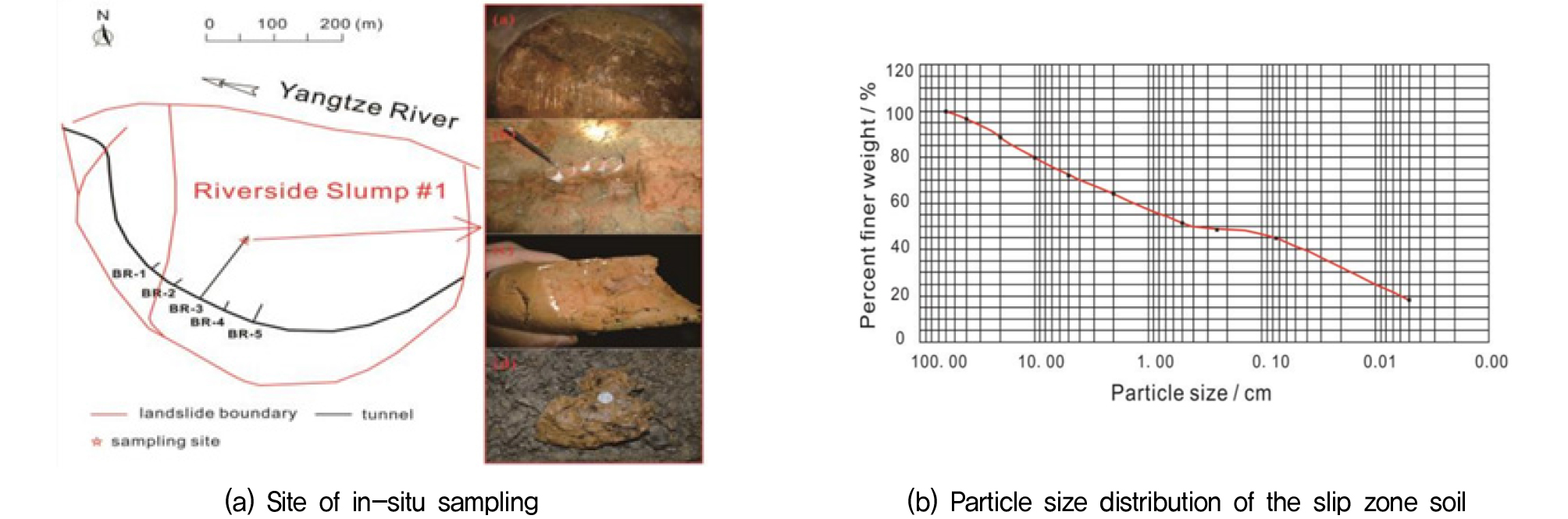
Chun & Yi(2020)는 양쯔강 주변 지역 토양이 장기간 포화상태에서의 강도특성을 분석하기 위해 사면이 붕괴된 지역에서 시료를 채취하여 분석하였다(Fig. 3). 시료의 경우 평균 수분함량이 9.8%, 건조밀도 2.07g/cm3, 점토 함량 64.7%, 평균 소성지수는 11.7, 입자 직경은 0.005~60mm, 는 300, 는 0.03임을 확인하였다.
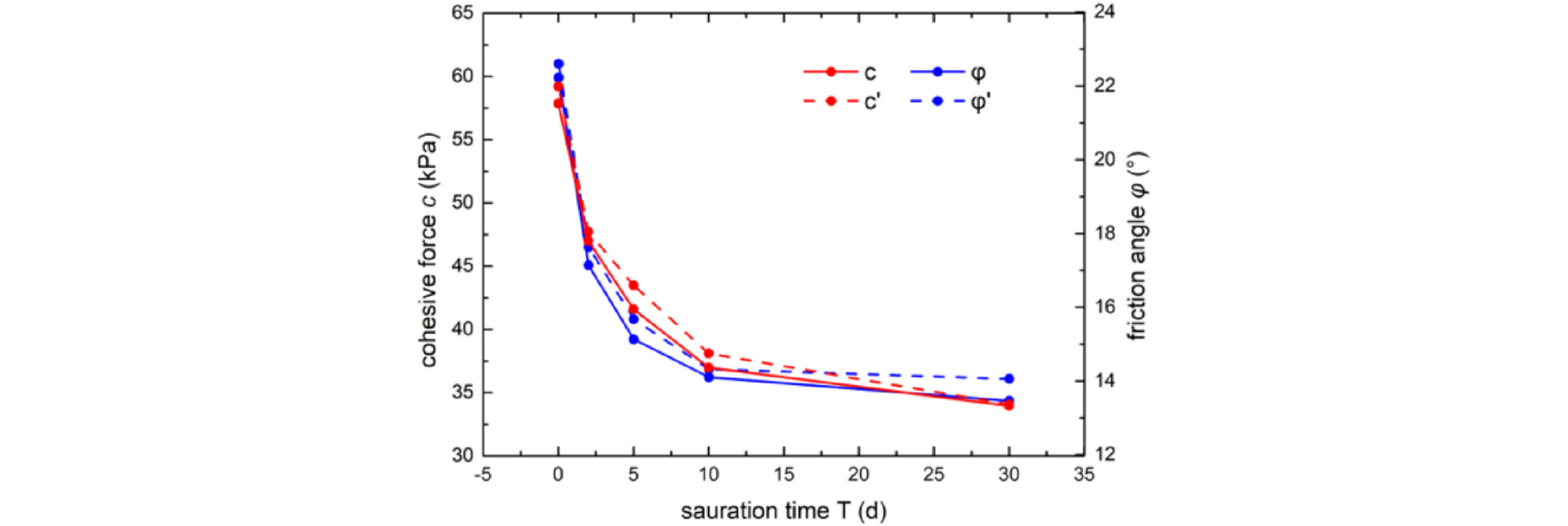
채취된 시료를 분석한 결과는 Fig. 4에 나타냈다. 그림을 보듯이 시간이 지남에 따라 점착력과 마찰력이 낮아짐을 확인하였다.
지반특성 분석을 통해 지반강도는 각각 다른 감소계수에 의해 동시에 감소한다고 가정된다. 따라서 Eq. (4)와 (5)로 나타낼 수 있다.
이때, 시간에 따른 변화하는 감소계수는 와 이며, 와 는 초기 접착력과 내부 마찰각을 나타낸다. 와 는 특정 시점에서의 감소된 접착력과 내부마찰각이다. 는 실험을 통해 얻은 계수이며, 실험을 통해 , , , , , 이다. 초기강도 강도 매개변수는 , 이다. 이를 통해 Eq. (6), (7)로 나타낼 수 있다.
2.2 지반 강도저하 모델 제안
앞서 언급된 문헌(Yoshida et al., 1991; Chun & Yi, 2020)을 통해 열화 인자를 분석하여 국내 지반조건에 따른 지하 생활기반시설 열화모델을 제시하고자 한다. 선행연구 분석 결과를 정규화 하여 Fig. 5에 나타냈다. Fig. 5에서 보듯이 실측데이터(왼쪽)를 정규화 하여 나타내었다(오른쪽). 이는 열화모델의 개발을 위해 지반의 물성치들의 포화도 정도에 따른 변화를 쉽게 접근해 볼 수 있다.
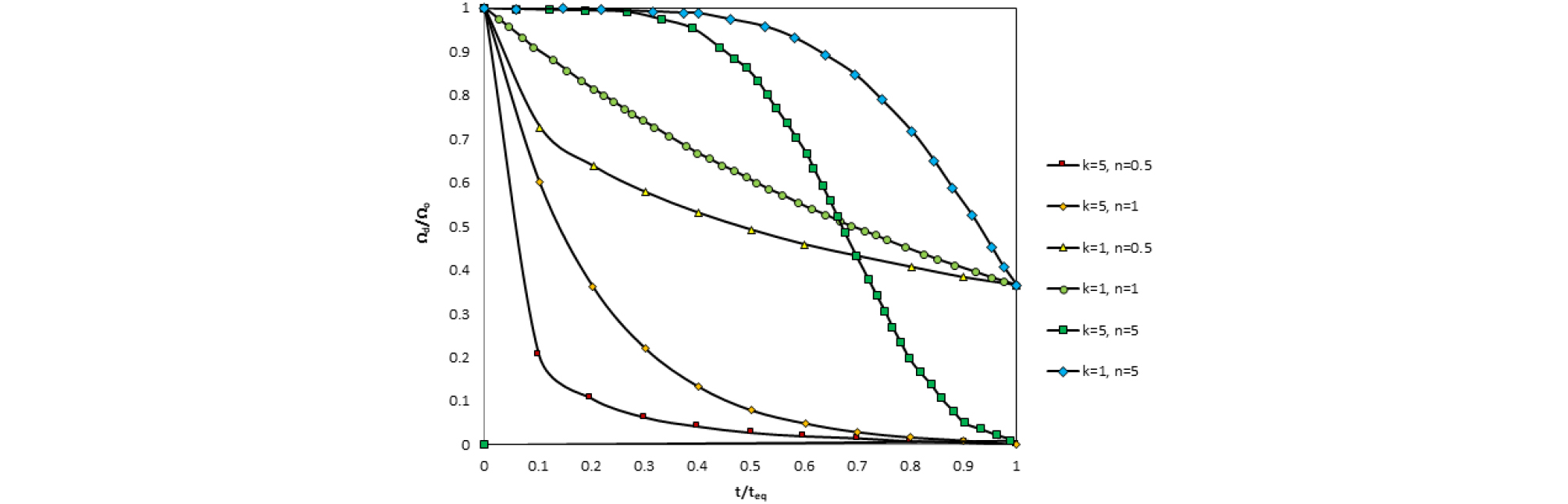
선행연구 분석 결과를 보듯이 시간의 경과에 따른 다양한 환경적인 요인(포화도의 변화, 풍화작용 등) 지반물성의 강도저하는 연구자들에 따라 다르게 제시하고 있다. 공통된 특징들을 살펴보면 강도의 감소가 exponential 함수를 따르고 있음을 알 수 있다. 따라서 본 논문에서는 보다 보편적인 지반열화를 표현하기 위해 Eq. (8)을 제시하였다.
여기서, : 저하된 물성치(변형계수, 강도정수)
: 초기 물성치(변형계수, 강도정수)
: 모델계수
: 지하구조물의 공용수명
: 지하구조물 설치 후 임의의 시간
본 논문에서 제시한 지반열화모델인 Eq. (8)에서 보는 바와 같이 초기 지반 물성치는 시간의 경과에 따라 기하급수적으로 감소한다고 가정하였다. 감소하는 모양은 모델계수인 n에 의해 결정되며, 지반물성치의 최종 값은 모델계수인 k에 의해 결정된다. Fig. 6은 본 논문에서 제시한 Eq. (8)의 다양한 모델계수에 따른 지반 열화 곡선을 나타냈다.
3. 열화모델을 활용한 지하생활기반시설물 장기거동 예측
3.1 강도정수 열화곡선
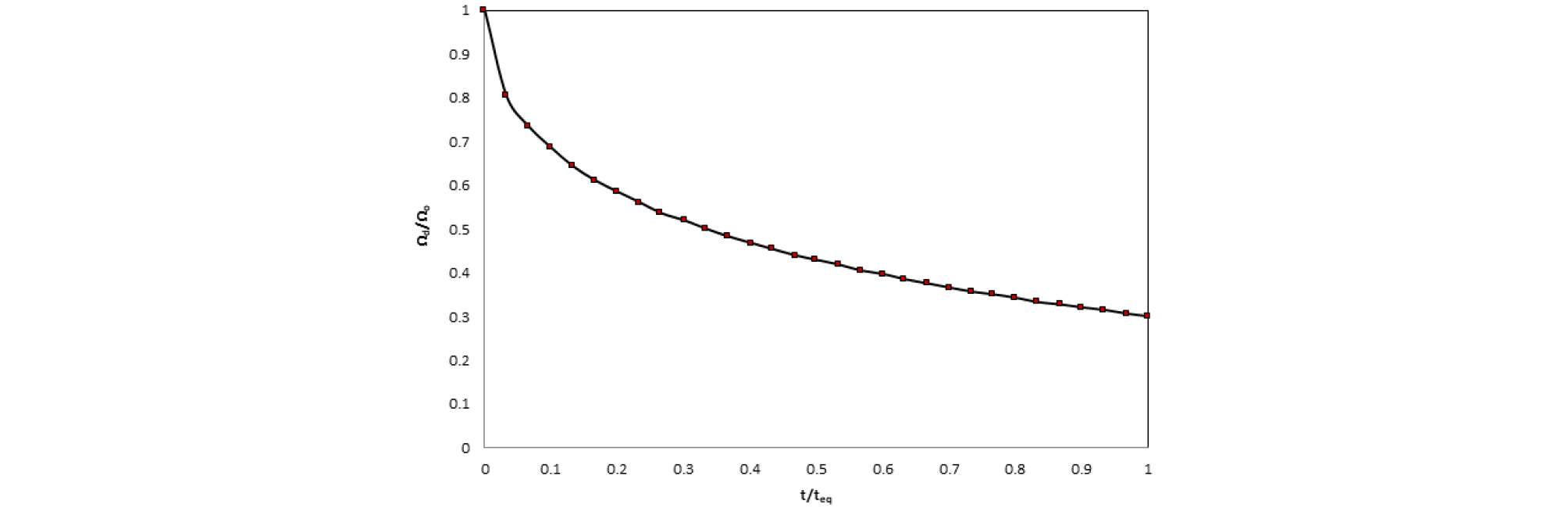
시간의 경과에 따른 강도정수의 열화 앞서 언급된 문헌 (Sato & Kamemure, 1984; Matsunaga, 2008; Yashiro et al., 2009; Sandrone & Labiouse, 2010)을 참조하여 사면의 공영기간까지 강도저하가 지속적으로 진행되어 최종적으로 초기강도의 30% 남는 것으로 가정하여 해석을 진행하였으며, 사면의 공용기간을 최대 시간은 30년을 기준으로 하여 정규화한 강도정수의 강도저하 그래프를 그리면 Fig. 7과 같다. 모델계수 k, n이 각각 1.2와 0.5인 경우이다. Fig. 7에서 보듯이 연속적인 강도정수의 감소값이 input값으로 입력되어 원하는 시간경과의 안전율 변화를 얻을 수 있다.
3.2 수치해석
열화모델을 활용한 지하생활기반시설물 장기거동을 예측하기 위해 유한요소 수치해석 프로그램인 ABAQUS를 이용하여 수치해석을 수행하였다. 유한요소 수치해석 프로그램인 ABAQUS는 해석모델 내 여러 가지 응력, 변형률 및 응력-변형률에 따른 반응지표에 대한 해석 결과 값을 구할 수 있다. 이를 통해 열화된 지반정수에 따른 지하구조물의 거동을 분석할 수 있으며, 각 매개변수가 지하생활기반시설물 거동에 미치는 영향을 확인할 수 있다. 수치해석에 사용된 지반물성치는 Table 1, Mesh는 Fig. 8에 나타냈다. 지반 물성치는 일반적인 사면의 물성치를 사용하였으며, 파괴모델은 Mohr-Coulomb 모델을 적용하였다. 또한 소성거동은 팽창각(dilation angle)을 고려한 non-associate flow rule을 적용하여 사면의 파괴면을 살펴보았다. 사면의 안전율은 강도감소법을 적용하여 계산하였다(Eq. (9)).
Table 1.
Material properties (unit, N.m)
| Density (N/m3) | E (N/m2) | V | C (N/m2) | Φ (°) | Ψ (°) |
| 1,920 | 4,000,000 | 0.3 | 10,000 | 34 | 17 |
여기서, cf=파괴 시 점착력, c=현재 점착력, =파괴 시 마찰각, =현재 마찰각
사면의 경우 임의의 사면으로 초기상태의 안전율이 비탈면 기준 1.5(Ministry of Land, Transport and Maritime Affairs, 2009)보다 높은 2.0으로 임의사면 형상을 구성하였다.
3.3 수치해석 해석결과
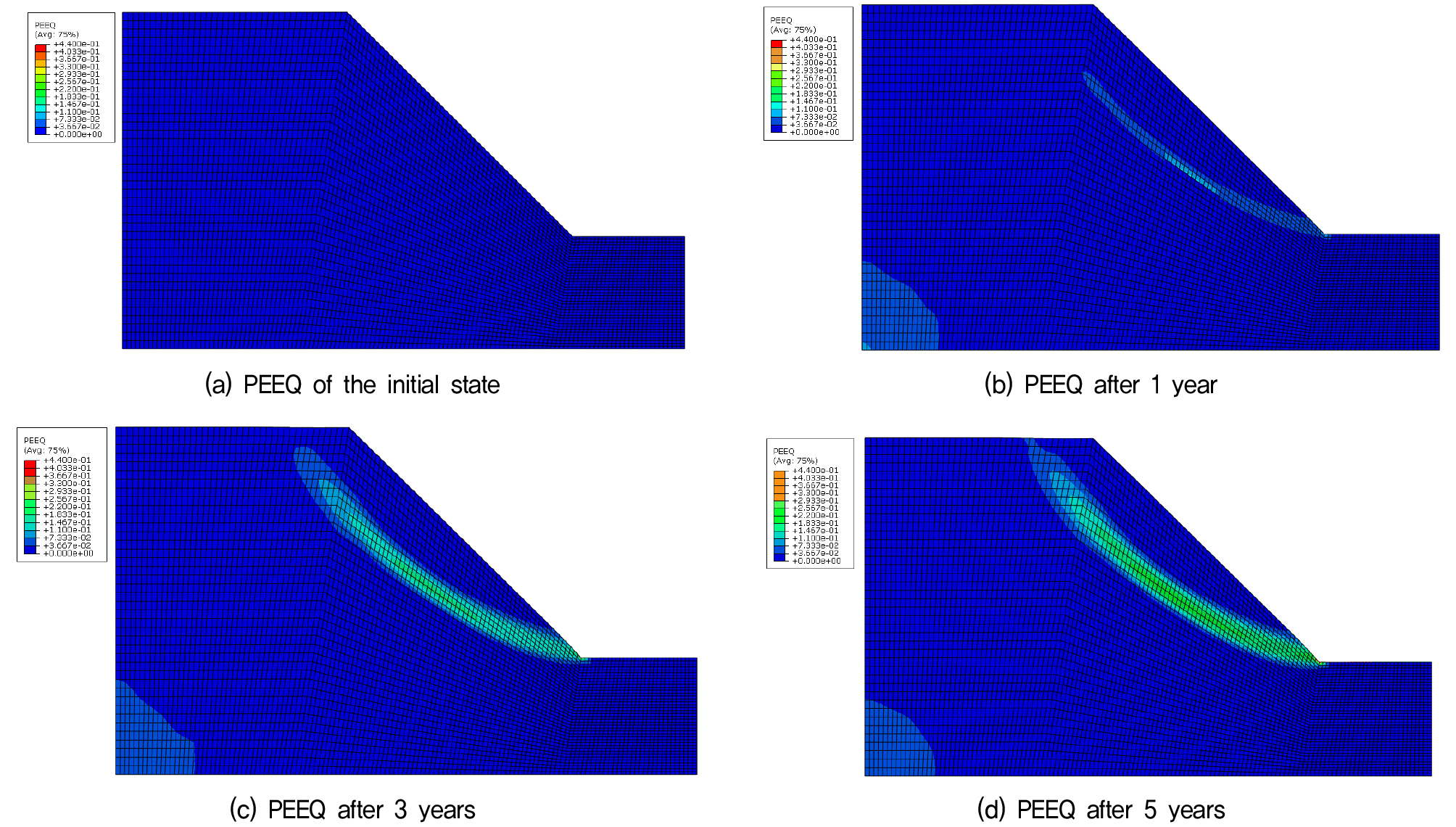
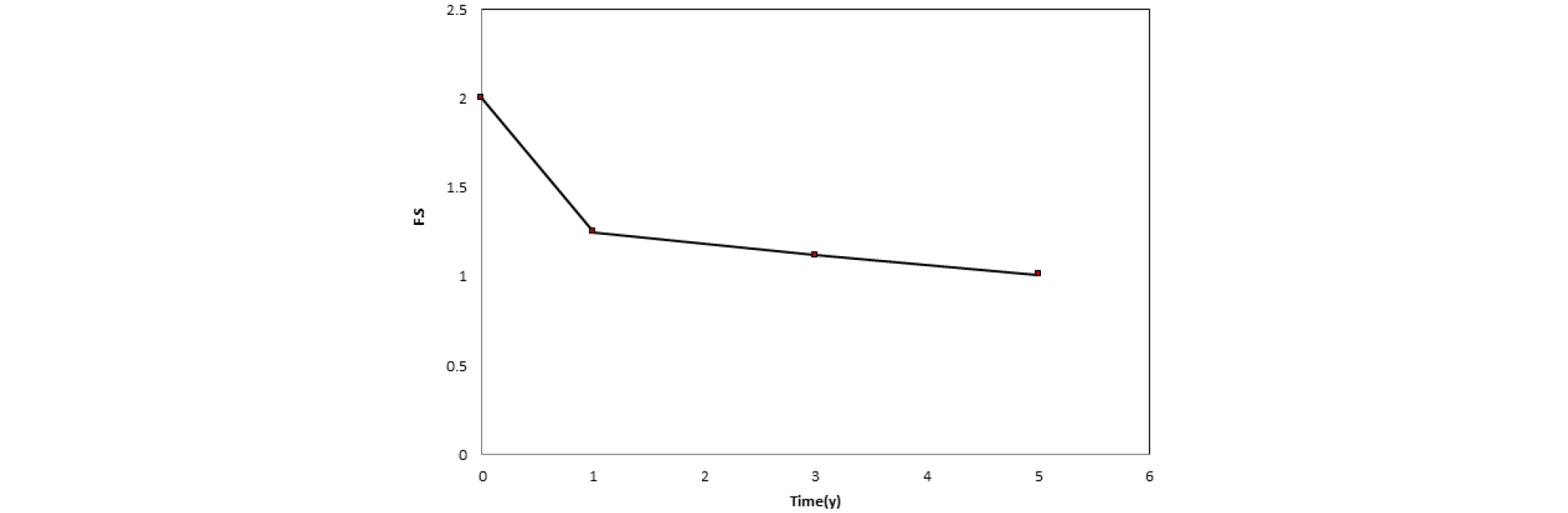
수치해석 결과는 Fig. 9와 10에 나타냈다. Fig. 9는 시간이 지남에 따른 등가소성변형률(PEEQ)를 나타냈다. 그림을 보듯이 파괴면이 시간이 경과함에 따라 파괴면의 모습이 뚜렸해짐을 알 수 있다. 이는 시간이 경과함에 따라 강도정수 값이 앞서 제시한 열화모델의 곡선에 따라 감소된 입력값이 자동으로 계산되기 때문이다. Fig. 10은 시간에 따른 안전율의 변화를 나타냈다. 그림을 보듯이 초기에는 안전율이 2.0으로 안전한 상태였으나, 1년 후 1.25, 3년 후 1.12, 5년 후 1.01로 시간이 지남에 따라 안전율이 낮아짐을 확인하였다. 안전율의 변화 또한 열화모델에서 제시된 강도정수 감소 경향에 따라 초기에 가장 많이 감소하고 이후 점차적인 감소를 보여줌을 알 수 있다. 따라서 본 논문에서 제시한 열화된 강도정수를 활용하여 시간에 따른 사면의 안전율 변화를 확인하였다.
4. 결 과
본 논문에서는 지하 시설물의 장기거동을 예측할 수 있는 열화모델 식을 제시하였으며, 수치해석 분석을 통한 검증하여 다음과 같은 결론을 얻었다.
(1) 선행연구 분석을 통해 국내 실정에 맞는 지반의 강도정수 열화모델 식을 제시하였으며, 열화된 강도 정수를 활용하여 시간경과에 따른 안전율 변화를 확인하였다.
(2) 사면의 안전율의 경우 초기안전율이 2.0의 임의사면으로 열화된 강도 정수를 활용하여 수치해석한 결과 1년 후 1.25, 3년 후 1.12, 5년 후 1.01로 시간이 지남에 따라 안전율이 낮아짐을 확인하였다.
(3) 시간경과에 따른 사면의 등가소성변형율(PEEQ)의 변화를 통해 사변의 파괴면이 뚜렷해지고, 파괴면이 선단에서 표층으로 진행됨을 알 수 있다.
(4) 따라서, 제시한 열화모델 식을 활용하여 다양한 지하 구조물의 시간에 따른 장기거동 예측이 가능할 것으로 보이며, 장기거동 예측을 통해 지하구조물의 보수, 보강 시기를 결정할 수 있을 것으로 예상된다.