1. 서 론
2. 유출의 기본이론 및 지배방정식
3. 모형유역형상 및 강우분포형
3.1 모형유역형상
4. 적용 및 분석
4.1 강우강도와 강우길이가 동일한 경우 정방형 유역에서의 유출분석
4.2 강우강도와 강우길이가 동일한 경우 장방형 유역에서의 유출분석
4.3 강우강도와 강우길이가 동일한 경우 신장형 유역에서의 유출분석
4.4 강우강도와 총 강우량이 동일한 경우 정방형 유역에서의 유출분석
4.5 강우강도와 총 강우량이 동일한 경우 장방형 유역에서의 유출분석
4.6 강우강도와 총 강우량이 동일한 경우 신장형 유역에서의 유출분석
5. 결 론
1. 서 론
최근 우리나라 뿐만 아니라 전 세계에 발생하고 있는 기후변화로 인하여 강우의 형태가 강우량, 강우발생시간, 강우강도 등 그 양상이 매우 다양하게 나타나고 있다. 이 영향으로 인해 유출 특징도 변하고 있는 상황이다.
이에 따라 강우-유출관계는 다양한 정보와 정밀한 모의에 의한 분석이 필요해지고 있다. 지표면유출은 강수량, 강우강도, 강우지속기간, 강우이동방향 및 이동속도와 같은 시·공간적특성과 지형의 모양, 크기와 같은 지형학적 영향을 받으며, 이런 특성과 영향을 나타내는 것이 홍수유출수문곡선이다. 특히 강우의 시간적, 공간적분포는 유출에 영향을 미치는 중요한 인자이다. 이와 같은 강우의 시간적, 공간적 분포는 이동강우의 진행방향, 이동속도 그리고 강우분포형에 의하여 나타내어질 수 있으며, 강우의 진행방향은 지표면에서 흐름방향을 기준으로 단순하게 상·하류, 횡방향 및 대각선 방향으로 나타낼 수 있다.
Maksimov(1964)에 의하여 처음 이루어진 이동강에 대한 연구는 강우의 이용이 첨두홍수량의 변화에 영향을 준다는 사실을 최초로 규명하였다. Marcus(1968)가 이동강우에 대한 실험적 연구를 한 이후 Roberts & Klingeman(1970)의 연구에 의해 강우의 이동방향에 따라 첨두홍수량이 변화하고 이동방향의 영향으로 수문곡선의 감수부에 영향을 미침을 밝혀내었으며, Surkan(1974)는 홍수량관측 자료를 이용하여 이동방향과 이동속도가 첨두홍수량과 평균유출율에 가장 큰 영향을 준다는 연구결과를 발표하였고, Lima & Singh(2003)는 토양유실에 영향을 주는 강우이동방향은 상류방향보다 하류방향 이동강우에 의하여 더 큰 영향을 준다는 연구결과를 발표하였다. Sargent(1981, 1982)는 이동방향과 이동속도가 첨두홍수량, 총유출량, 홍수수문곡선 등에 미치는 영향을 검토하였다. Richardson(1989)이 1차원 유한요소법으로 이동강우를 분석한 결과를 제시하였으며, Ogden & Richardson(1995)이 이동속도와 이동강우길이를 무차원화하여 2차원 강우-유출모형을 이용 유출을 모의한 연구에 이어 Singh(1997, 1998, 2002a, 2002b)에 의해 이동강우에 대한 많은 연구가 발표되었다. 국내에서는 Choi et al.(1992)은 이동강우해석을 위해 분포형모델을 개발하여 연구한 결과가 있고, Choi et al.(2000)은 실제유역에서 GIS를 이용하여 이동강우의 유출특성을 연구하였으며, Han et al.(2004), Han et al.(2006)에 의해 작은 유역에서의 유출특성과 이동강우와의 관계를 나타내었다. Park & Yoo(2017)은 호우의 방향성과 유역의 유출응답특성과의 관계를 평가하였다.
지금까지의 이동강우와 관련된 국내·외 연구동향은 주로 이동강우의 시간분포, 이동방향, 속도에 따른 첨두홍수량, 첨두홍수량 발생시간, 유출총량, 수문곡선의 형태에 관한 연구가 주된 연구방향이다. 연구방법은 관측 및 실험적 연구, 해석적 방법이 모두 적용되고 있다.
이동강우는 시·공간적으로 변화하는 특징을 가지는 자연현상으로서 이에 따른 강우-유출해석은 매우 어렵고 현재 사용하는 여러 해석방법에 한계가 있다. 일반적으로 강우-유출해석 시 정체된 특성을 가지는 정지강우로 해석하고 있으나 최근에 발생되는 극한호우로 인하여 대규모 홍수피해가 증가하고 있는 기상상황을 감안한다면 본 연구에서 제시되는 이동강우의 특성을 파악하는 것은 매우 중요한 연구이다. 이동강우의 속도와 유역을 매우 작은 소규모로 정하여 모형화한 연구가 있으나 본 연구에서는 그 크기를 1,000m×1,000m로 하여 보다 큰 유역에서의 유출현상에 대하여 분석하여 향후 호우 시 발생하는 실제 소유역에서의 유출특성과의 비교를 하고자 한다. 유역의 출구점을 유역의 정중앙에 위치하는 대칭형으로 정하고 출구점을 기준으로 하여 가로·세로길이가 같은 정방형유역, 가로방향의 크기가 큰 장방형유역, 세로방향의 길이가 긴 신장형유역을 비교하였고, 강우이동속도와 강우이동방향을 상류, 하류, 횡방향, 대각선방향 4가지로 다양하게 모의하여 유출수문곡선을 작성하여 그 특성을 다양한 이동속도에 대하여 비교·분석하였으며, 강우분포형은 균등분포형, 전진형, 지연형, 중앙집중형 4가지 형태에 대하여 비교·분석하였다. 분석 시 적용한 지배방정식으로는 부정부등류 흐름인 홍수 시 지배방정식인 Saint-Venant 방정식으로부터 유도된 운동파이론을 이용하였다.
2. 유출의 기본이론 및 지배방정식
하천의 홍수류와 지표면에서의 흐름은 시간적, 공간적으로 변하는 부정부등류를 이루게 된다. 강우로 인한 지표면유출은 하천으로의 측방유입이 되며, 개수로 흐름문제에서 비정상흐름으로 간주될 수 있다. 1차원 비정상 개수로흐름의 지배방정식은 연속방정식과 운동량방정식으로 구성된 Saint-Venant 방정식이다.
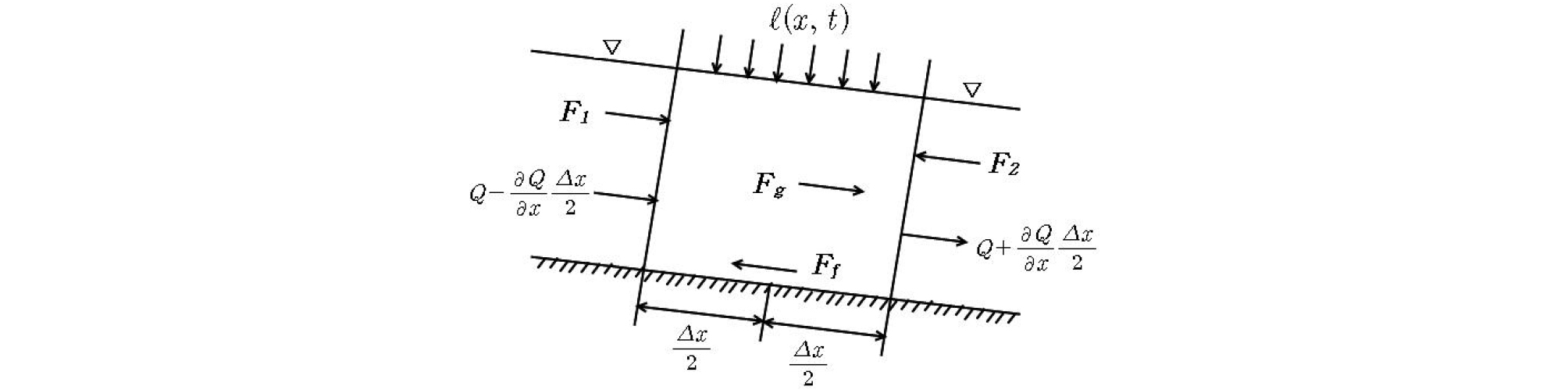
보존식형태의 Saint-Venant 방정식을 사용하여 관성력과 압력항을 무시할 경우 운동파가 흐름을 지배하게 되며, 지표면흐름과 하도흐름에 대한 연속방정식과 운동량방정식의 유도를 위한 흐름요소들은 Fig. 1과 같다.
여기서, Fg는 중력의 흐름방향 성분력, Ff는 흐름단면의 윤변에 작용하는 마찰력이고, F1는 유입단면에서의 전수압, F2는 유출단면에서의 전수압이다.
부정부등류의 연속방정식은 어떤 하도구간으로 흘러들어오는 유입량과 흘러나가는 유출량의 차이가 구간의 저류량변화율과 같아진다는 질량보존의 원리를 성립시켜 준다. 이는 Eq. (1)과 같은 수문연속방정식으로 나타난다.
여기서, IF=유입량, Q=유출량, S=저류량이다.
측방유입량(lateral inflow)을 가지는 하도구간이 일 때의 자연하도는 Fig. 1과 같으며, 유입량은 , 유출량은 , 저류량의 변화율은 이 된다.
이를 Eq. (1)에 대입하면 Eq. (2)와 같은 구간 에 대한 부정부등류의 연속방정식이 되며, Eq. (2)를 단위 폭당 유량에 대한 연속방정식으로 바꾸면 Eq. (3)과 같아진다.
여기서, t=시간(sec), x=흐름방향으로의 거리(m), h=수심(m), A=흐름단면적(m2), Q=유출량(m3/s), q=단위폭당유출량(m2/s), =구간에 시간동안의 평균 강우유입량(m2/s), =단위폭당의 강우유입량(m/s)이다.
다양한 속도로 이동하며, 내리는 강우는 지표면에서 측방유입이 되며, 부정류 개수로 흐름문제로 해석될 수 있다. 지표면흐름은 연속방정식과 운동량방정식으로 구성된 Saint-Venant방정식에 의하여 표현될 수 있으며, 보존식형태의 Saint-Venant 방정식은 관성력과 압력항을 무시할 경우 운동파가 흐름을 지배하고, 1차원흐름의 경우 지표면흐름에 대한 연속방정식은 Eq. (4)와 같게 된다.
여기서, =시간(sec), =지표면 흐름방향으로의 거리(m), =단위폭당 유량(m3/sec/m), =지표면 수심(m), =측방유입량으로서 지표면유출의 경우 공간적, 시간적으로 변화하는 유효강우(m/s)로 해석된다.
해석의 단순화를 위하여 지표면은 침투가 발생하지 않는 불투수층으로 가정하였고 지표면 경사는 완만하고 흐름은 1차원흐름이라 가정한다. 가정에 따라 지표면흐름은 수심의 함수로 나타내어 Eq. (5)와 같은 운동량방정식으로 표시할 수 있다.
여기서, 와 β는 경험적 상수이며, Manning 의 등류공식을 적용하면 와 β는 각각 =, β=5/3 이며, n=조도계수, =마찰경사이다.
Eq. (4)의 연속방정식과 Eq. (5)의 운동량방정식이 지표면흐름의 지배방정식으로 사용되며, 두 식을 연립방정식으로 풀어 q와 h를 구하였다. Eq. (5)를 시간 t에 대하여 편미분하여 Eq. (4)에 대입하면 운동파방정식 (6)을 얻을 수 있으며, 이때, Vp는 지표면흐름의 평균유속이다.
유한차분법을 이용하여 운동파방정식을 수치해석하는 방법에는 여러가지가 알려져 있으나, 2차해석 정도보다 안정성이 있는 1차해석 정도 수치해법을 사용하여 Eq. (6)을 이산화시키면 Eq. (7)과 같다.
여기서, 지표면 흐름의 Courant수 C는 Eq. (8)과 같으며, 이때 지표면흐름에 대하여 forward-in-time, backward-in-space차분법을 사용하였으며, 균일한 해를 얻기 위하여 Courant 수는 C≤1의 조건인 경우에만 안정된 해가 얻어진다. 여기서 i=공간격자점, n=시간격자점을 나타낸다.
이동강우의 경우-유출을 모의하기 위하여 로 이산화한 지표면을 시간씩 강우를 이동시켜서 유출모의를 하였고, 강우의 이동속도는 로서 나타난다.
3. 모형유역형상 및 강우분포형
3.1 모형유역형상
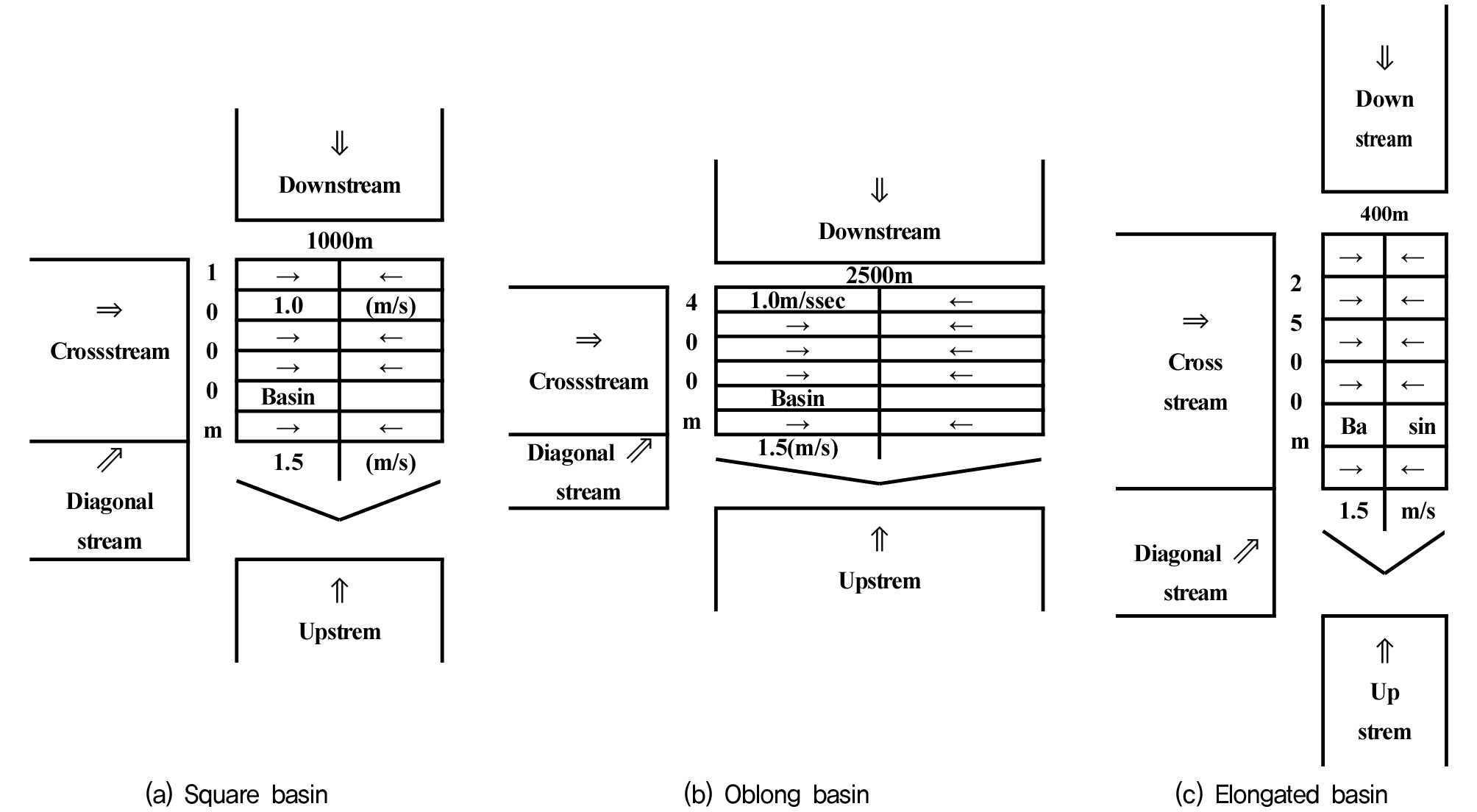
유역의 모양은 그 형상이 매우 다양하고 불규칙적인 모양으로 나타나기 때문에 유출특성의 해석을 위해서는 지표면을 단순화하여 해석하는 것이 편리하다고 할 수 있다. 그러므로 유출의 특성을 분석하기 위해 유역의 모양을 크게 3가지로 나누어 각각 가로세로의 길이가 같은 정방형유역, 가로방향의 길이가 긴 장방형유역, 세로방향이 긴 신장형유역 등으로 구분 지어 분석하였다. 이때 유역형상계수 F(=A/Z2)는 A를 유역면적, Z는 유로연장으로 정방형유역은 F=1, 장방형유역은 F>1, 신장형유역은 F<1이다.
유역의 면적은 모두 동일하게 106m2로서 정방형유역(F=1)은 가로 1,000m, 세로 1,000m, 장방형유역(F=6.25)은 가로 2,500m, 세로 400m, 신장형유역(F=0.16)은 가로 400m, 세로 2,500m로 정하였다. 유역의 형태와 인자들을 Table 1에 나타내었다.
Table 1.
Type of basin model
Model Factor | Square | Oblong | Elongated |
| Form |  |  |  |
| Basin shape factor (F=A/Z2) | 1 | 6.25 | 0.16 |
3가지 형태의 유역 모두 2개의 직사각형 형태로서 이루어진 유역으로 가정되었고, 지표면에서의 유출은 2개의 직사각형 사이에 있는 수로로 유입되어 하구방향으로 유출되는 것으로 정하였다. 이때 수로에서의 유출속도는 홍수 시 발생할 수 있는 1.5m/s로 정하였고, 모형유역의 크기 및 강우이동속도를 고려하여 지표면으로 유입되는 속도는 1.0m/s로 가정하였다. 이 모형을 Fig. 3에 나타내었다.
본 연구는 유역의 중심으로 하도가 형성되어 유출이 발생하는 대칭유역으로 정하였다. 본 연구에서는 강우가 모형유역의 왼쪽, 상류부, 하류부에서 접근하며, 대각선방향은 좌측하부에서 접근하는 것으로 가정하였다. 정방형의 경우 중심부인 500m, 장방형은 1,250m, 신장형의 경우는 200m로 나누어 분석하였다. 분석에 사용한 모형의 개략도를 Fig. 2에 나타내었다. 이와 같이 3가지 모형의 대칭형상의 모형유역에 대하여 거리별로 시간이 일정한 강우가 유역위를 다양한 속도로 횡방향, 하류방향, 상류방향, 대각선 방향 4가지 방향으로 이동하는 경우로 가정하고 이로 인한 유출의 특성을 분석하고자 한다.
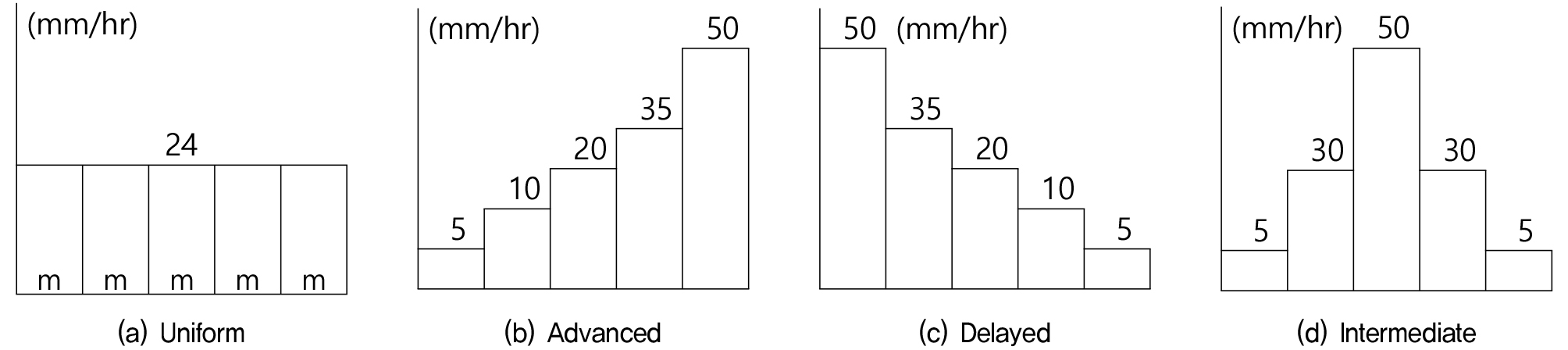
상류방향의 경우는 수로의 방향과 역방향으로 이동하는 것으로 분석하였고 대각선 이동은 횡방향과 상류방향이 동시에 시작해서 모형으로 진입하는 것으로 가정하여 이동하는 것으로 분석하였으며, 그 이동시간과 이동거리는 일치시켜 분석하였다. 강우이동이 하류방향으로 이동하는 강우의 경우, 상류지점에 내린 강우는 유출방향으로 이동하여 지표면출구에서 유출로 나타나며, 상류방향으로 이동하는 경우는 하류방향으로 이동하는 경우와는 반대로 지표면출구에서부터 유출이 시작되므로 역방향으로 유출을 계산한다. 대각선방향으로의 강우이동은 상류방향과 횡방향으로의 강우가 동시에 시작하여 모형으로 유입되는 것으로 가정하여 분석하였고 그 이동시간과 이동거리는 일치시켜 분석하였다. 유역의 크기가 유역의 유출특성에 영향을 미치는 점을 고려하여 모형유역의 크기를 정하였다. 본 연구에서는 4가지 강우분포형을 시간적으로 일정하다고 가정하고 일정한 크기를 갖는 강우강도가 3가지 대칭유역모형을 이동하는 경우에 대한 유출의 특징을 분석하였으며, 유효강우만을 이용하여 분석하였다. 균등분포형, 전진형, 지연형, 중앙집중형 4가지 강우분포형으로 분석하였으며, 모든 분포형의 강우강도는 동일(120mm/hr)하다고 정하였으며, 강우의 이동길이는 1,000m로 계산하였다. 이때 적용한 강우의 공간적 분포형을 Fig. 3에 나타내었다. 이때 x축은 강우의 길이를 나타내고 있다. 균등분포형의 경우는 강우전반에 걸쳐 고르게 분포하는 형태이며, 전진형의 경우 강우시작 전반부분에 높은 강도를 가지고 있고, 지연형은 강우 후반부분에 높은 강도를 가지고 중앙집중형은 강우 중앙부분에 높은 강도를 가지고 있는 특성이 있다. 일반적으로 중앙집중형이 가장 큰 첨두유량을 발생시킨다고 알려져 있다.
이동강우로 인한 유출을 분석하기 위하여 로 이산화시킨 지표에 대하여 시간씩 강우가 이동하는 것으로 가정하여 유출추적을 하였다. 강우의 이동속도는 에서 를 변화시켜 분석하였다. 강우이동속도는 매우 다양하게 나타나며, Ngirane-Katashaya & Wheater(1985)는 0.156~20m/s 범위의 강우이동속도를 사용하여 유출영향분석을 하였다.
위와 같이 강우강도와 일정한 강우길이를 가지고 있는 강우가 유역을 이동할 때는 강우이동속도에 따라 유역 내 발생하는 총강우량은 달라진다. 본 연구에서는 모형유역의 크기를 고려하여 이동속도범위 1.25, 2.5, 5.0, 10.0m/s에 대해서 비교·분석하였다.
이동속도가 변하는 경우 그 유역에 발생하는 총유출량도 변하게 된다. 이동속도에 따른 총유출량의 값을 Table 2에 나타내었다. 이때 유역위를 지나는 강우길이는 1,000m로 정하여 계산하였다. 이동강우강도의 크기는 4개의 강우분포형 모두 동일하며, 강우이동속도가 느릴수록 총유출량은 크게 나타나고 이동속도가 빠를수록 총유출량의 값은 매우 작아짐을 알 수 있다.
4. 적용 및 분석
4.1 강우강도와 강우길이가 동일한 경우 정방형 유역에서의 유출분석
정방형유역은 가로세로의 길이가 동일하며, 모형유역의 중심으로 유입되는 길이가 좌우, 상하가 같아 중앙집중형 강우분포의 경우 첨두시간을 중심으로 좌우가 대칭을 이루는 것이 특징인 유역이다.
강우이동속도는 변하더라로 강우강도와 유역을 지나는 강우길이는 변하지 않고 강우이동속도에 따른 총강우량의 차이가 발생하면서 유출이 발생하는 것으로 가정하여 분석하였다.
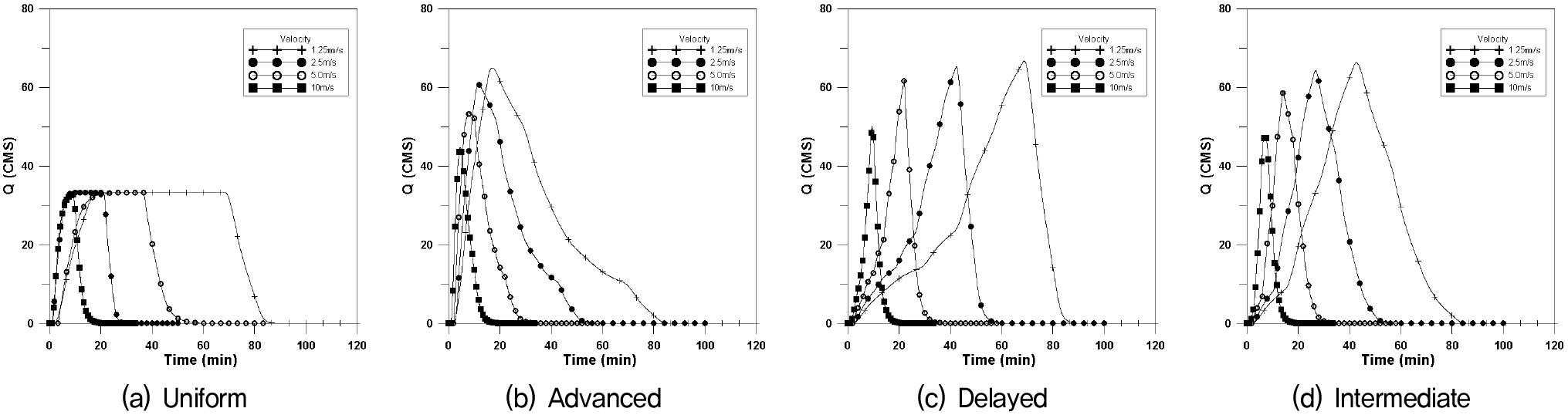
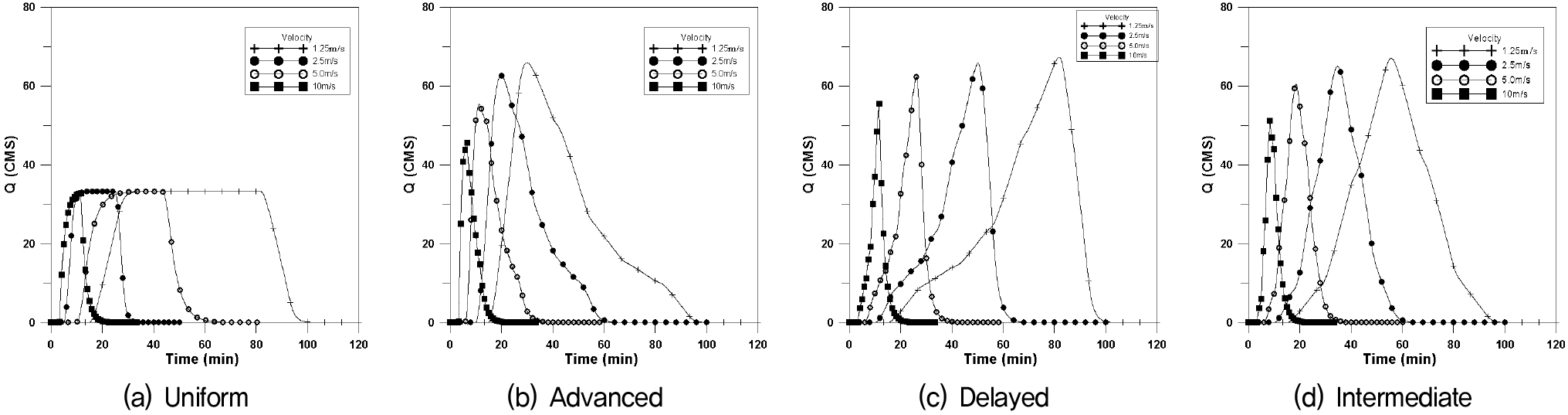
균등강우분포는 첨두유량이 강우이동속도가 느릴수록 길게 나타나며, 이동속도가 느릴수록 짧게 나타나고 있다. 전진형의 경우는 상승부분이 급한 경사를 나타내며, 감수곡선은 완만하게 나타나는 형태이고 지연형의 경우는 그 반대로 나타나고 있다. 4가지의 모든 이동방향에 대하여 비슷한 유출수문곡선 형태를 보이고 있다.
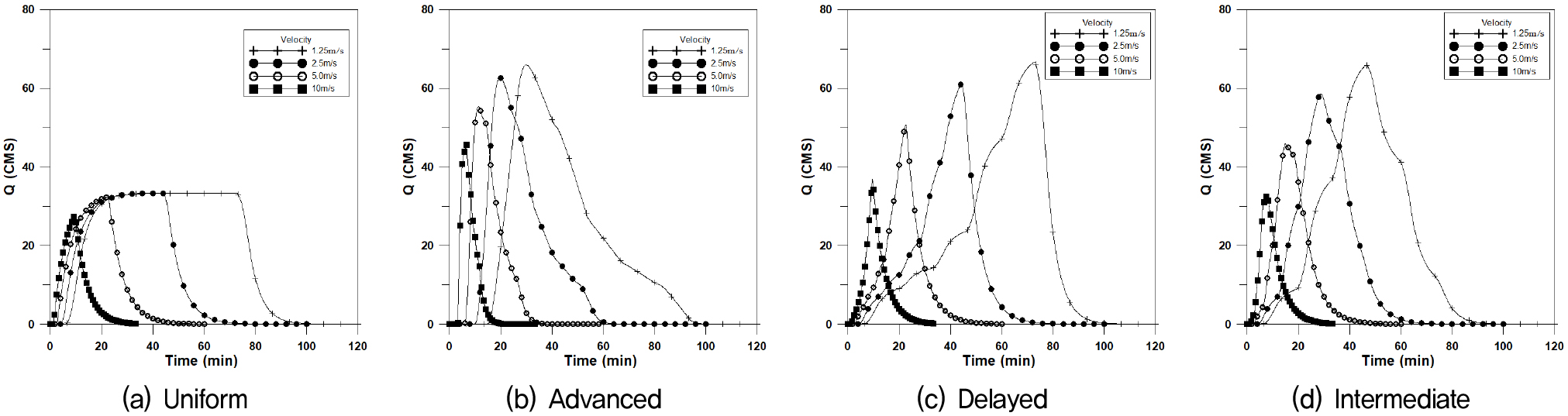
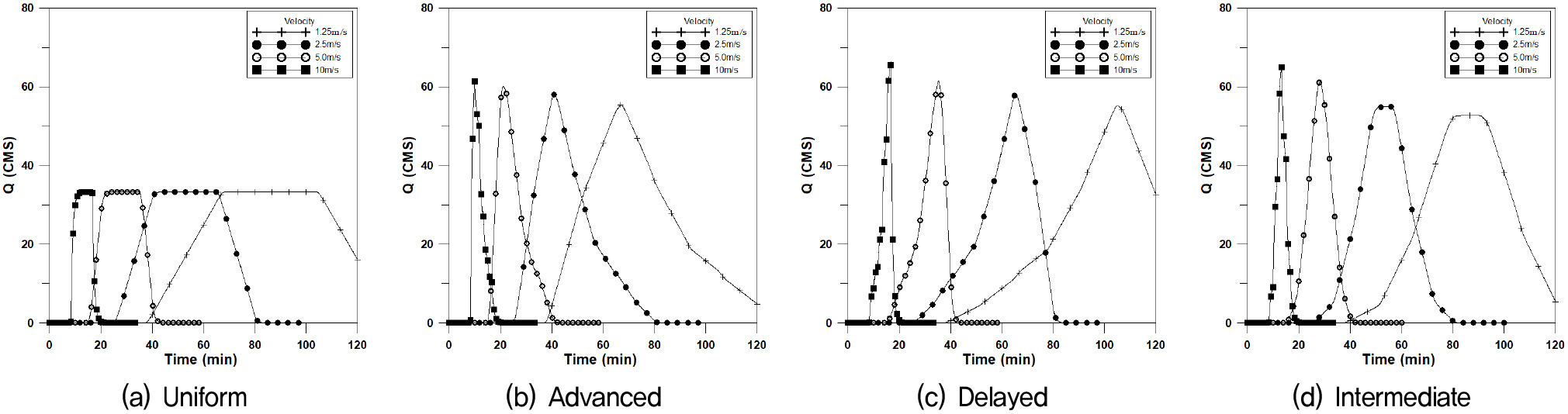
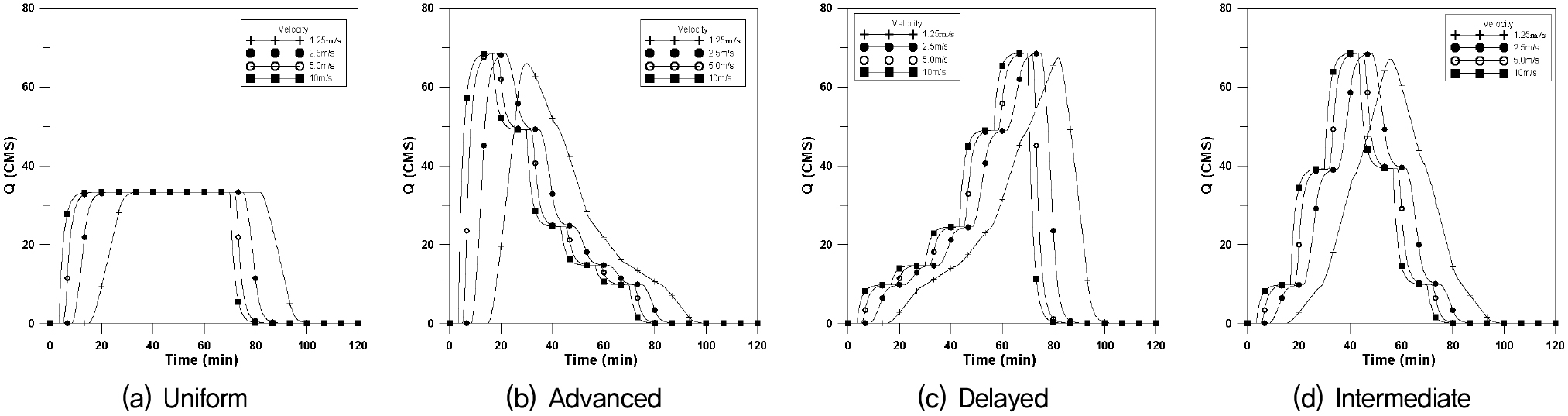
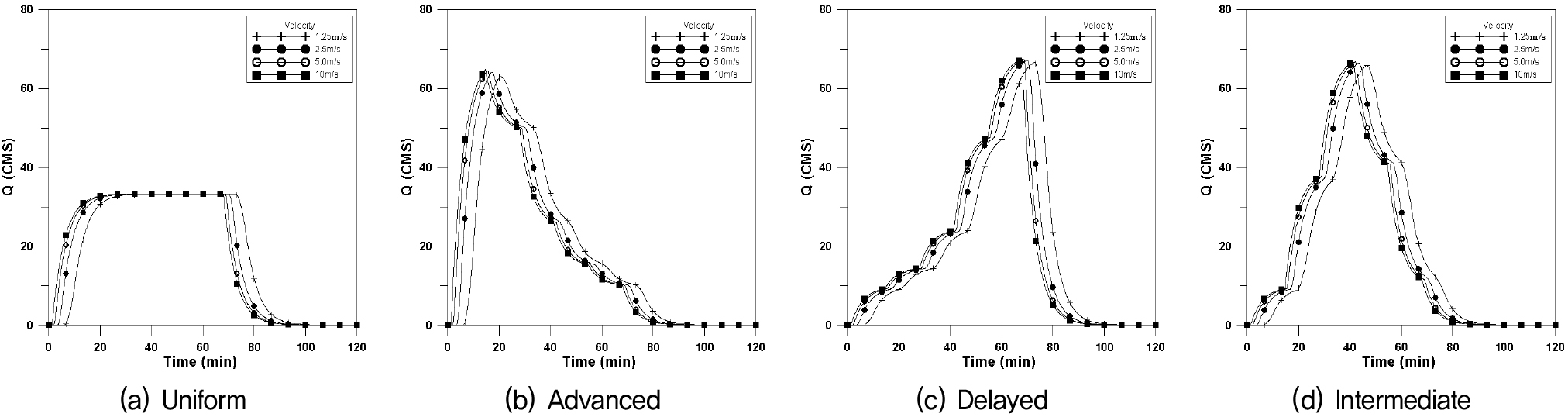
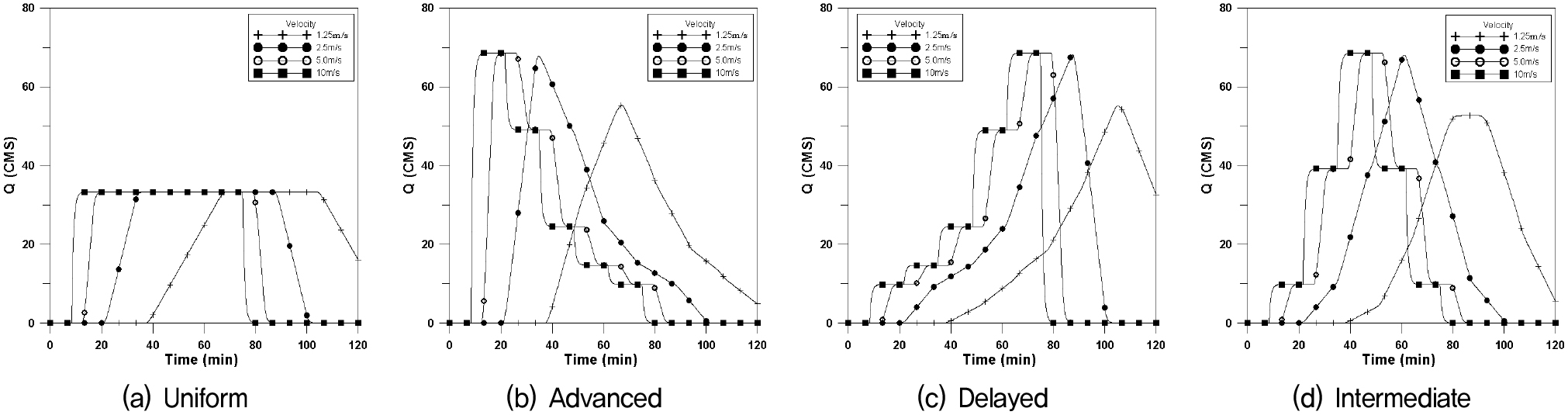
Fig. 4는 횡방향에 대한 수문곡선이며, Fig. 5는 하류방향, Fig. 6은 상류방향, Fig. 7은 대각선방향에 대한 4개의 강우이동속도에 대한 수문곡선을 나타내었으며, 이에 대한 첨두유량과 첨두시간은 Table 3과 같다.
Table 3.
Peak discharge and peak time in a square basin (Equal Intensity at equal rainfall length)
균등분포형의 경우 첨두유량은 거의 같은 값을 나타내고 있으나 이동속도가 빠를수록 첨두시간은 짧아지며, 특히 상류방향에서의 첨두시간의 차가 크게 발생되고 있으며, 하류방향 지연형에서의 첨두유량이 가장 크게 발생하고 있다.
4.2 강우강도와 강우길이가 동일한 경우 장방형 유역에서의 유출분석
장방형유역은 유역형상계수가 F(=A/Z2) >1 인 경우이며, 이때의 수문곡선의 상승부분은 급격한 경사를 이루며, 감수곡선은 완만한 경사를 가지는 것이 특징인 유역형태이다.
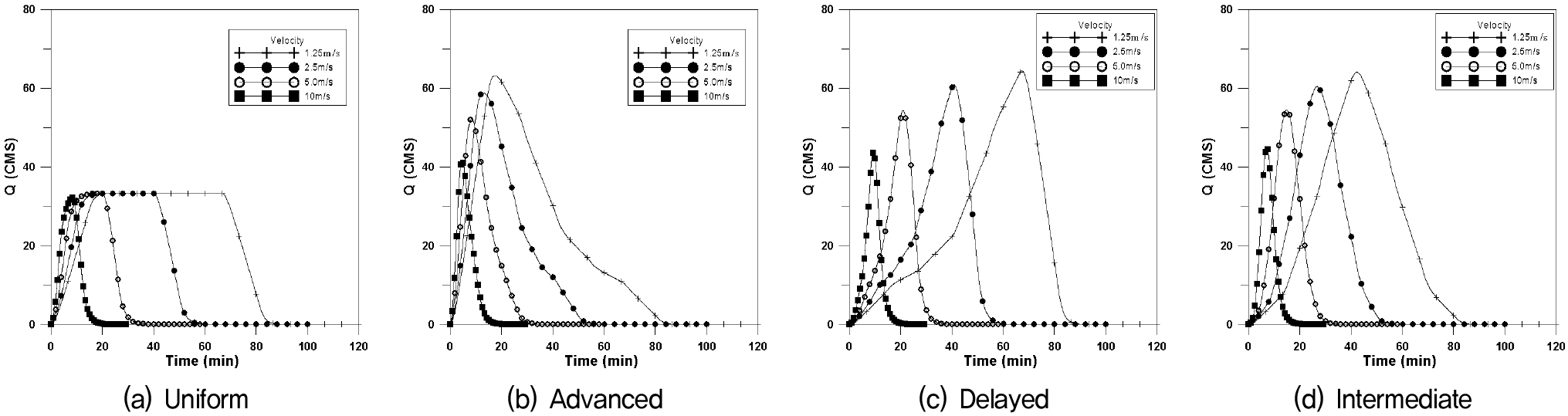
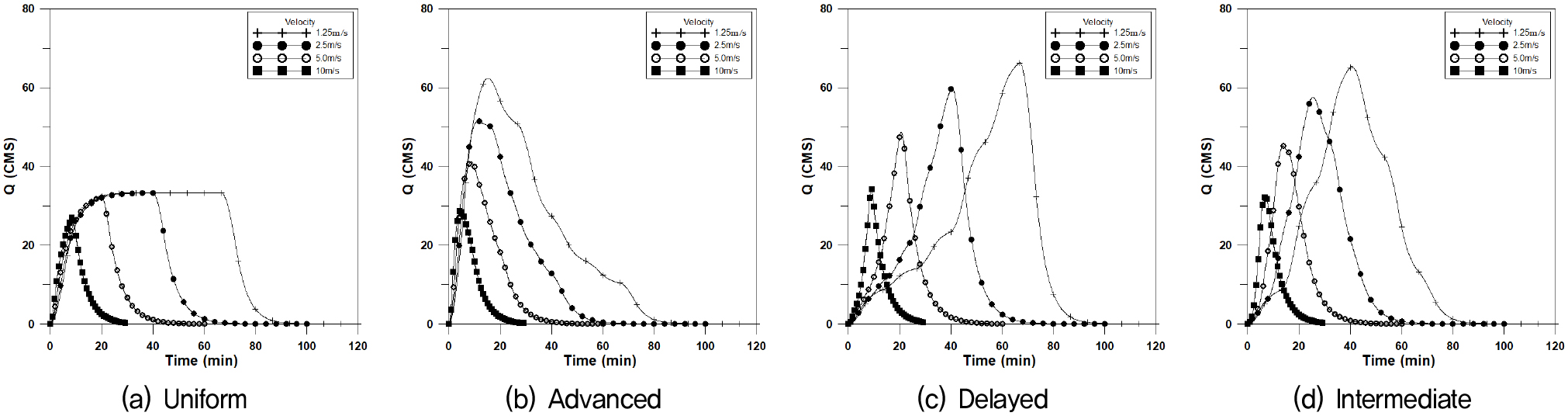
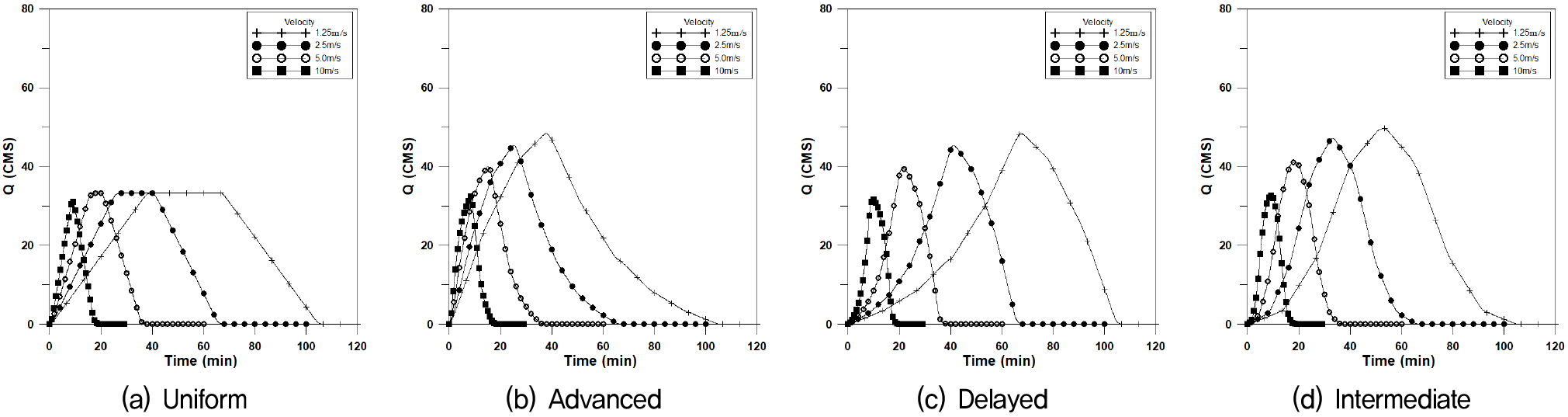
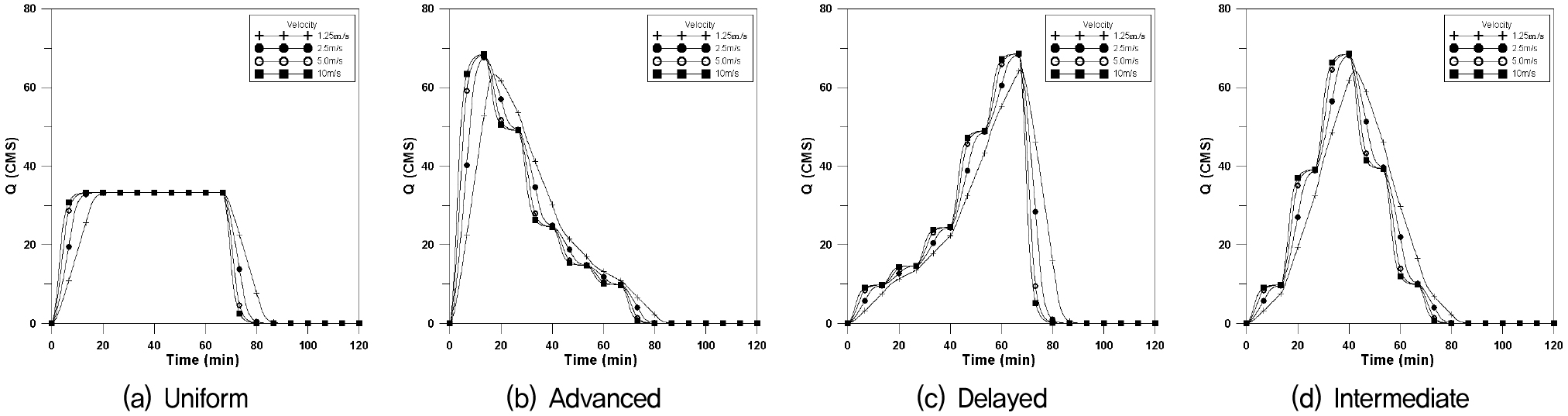
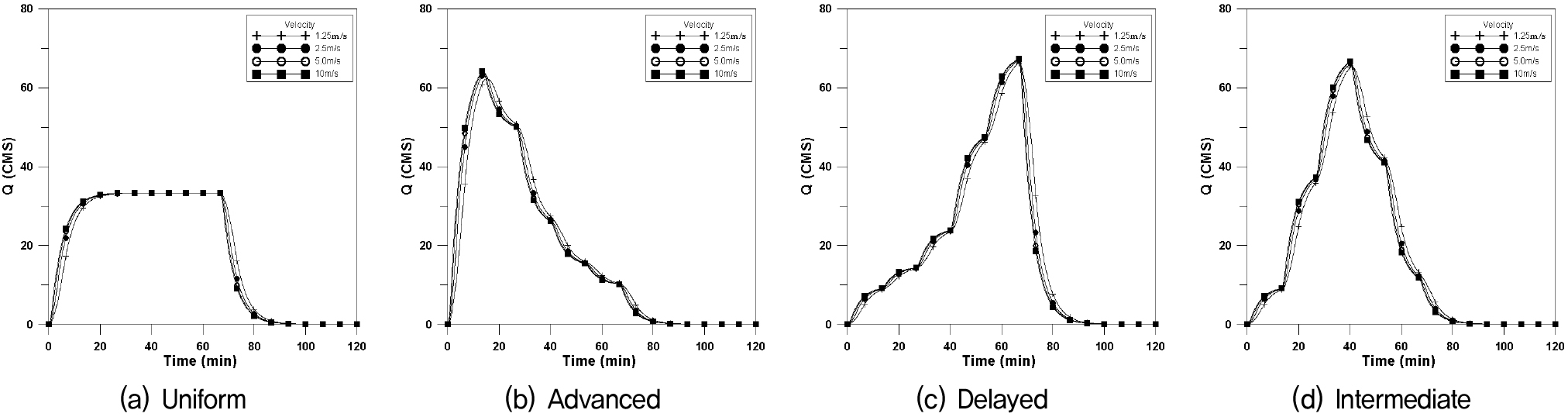
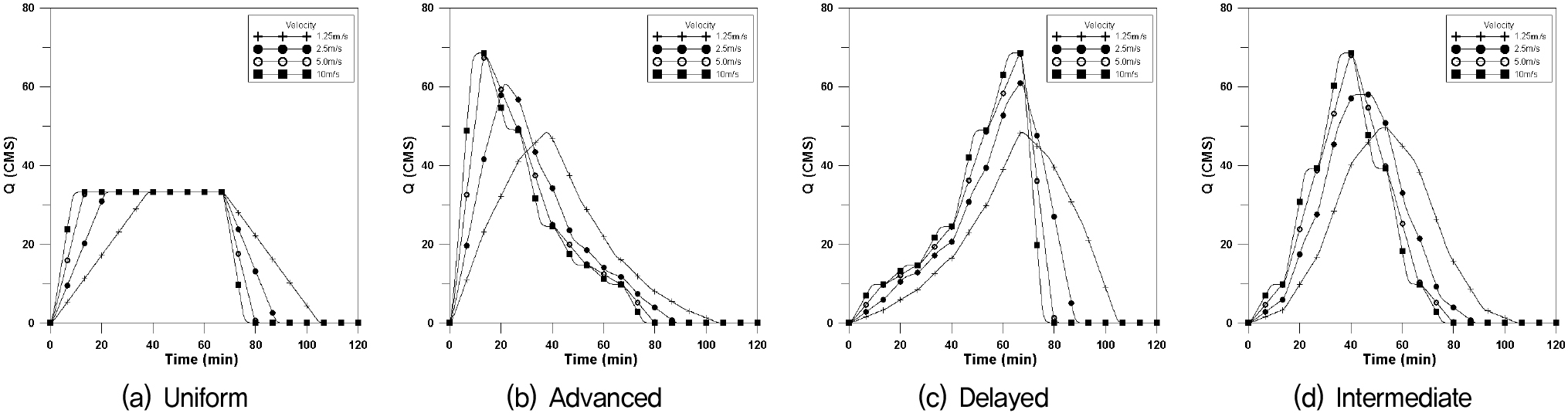
도달시간이 신장형유역에 비하여 짧으므로 첨두유량이 일어나는 시간이 짧아지고 첨두유량이 커진다. 본 연구에서는 폭 2,500m×길이 400m (F=6.25)인 장방형유역에 대하여 4개의 강우이동속도에 대하여 Fig. 8은 횡방향에 대한 수문곡선이며, Fig. 9는 하류방향, Fig. 10은 상류방향, Fig. 11은 대각선방향에 대한 수문곡선을 나타내었으며, 이에 대한 첨두유량과 첨두시간은 Table 4와 같이 나타내었다.
Table 4.
Peak discharge and peak time in a oblong basin (Equal Intensity at equal rainfall length)
장방형의 경우에도 균등분포형의 경우 첨두유량은 거의 같은 값을 나타내고 있으나, 이동속도가 매우 빠른 10.0m/s인 경우 이동강우 방향에 따라 첨두유량의 차이가 발생하고 있다. 지연형 강우분포에서 첨두유량이 크게 발생하고 있다.
4.3 강우강도와 강우길이가 동일한 경우 신장형 유역에서의 유출분석
신장형유역은 유역형상계수가 F(=A/Z2) <1 인 경우이며, 이때의 수문곡선의 상승부분은 장방형과 반대로 완만한 경사를 이루며, 감수곡선은 상승곡선에 비하여 급한 경사를 가지는 것이 특징인 유역형태이다.
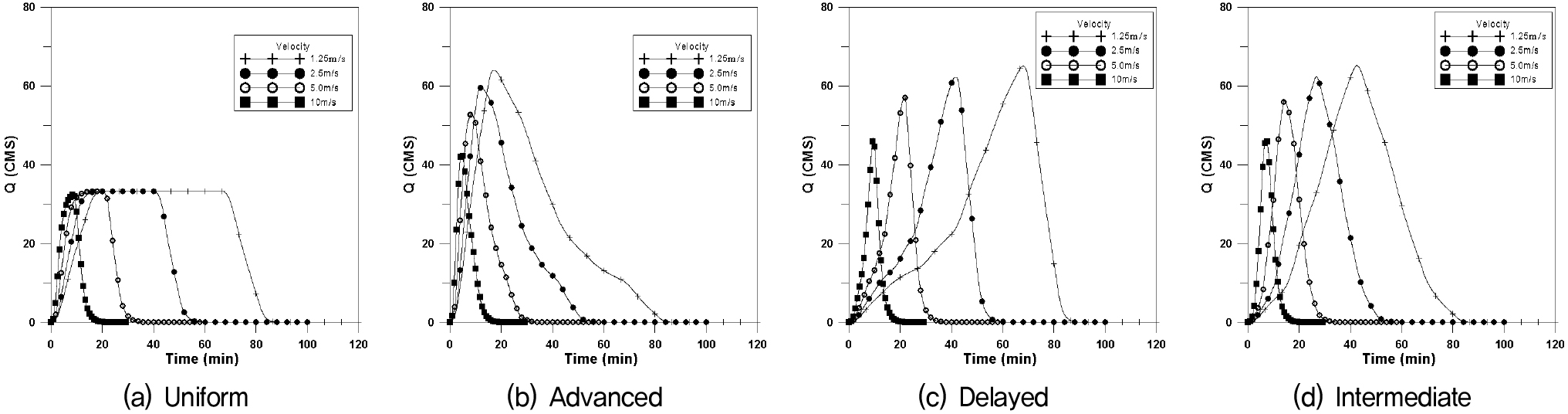
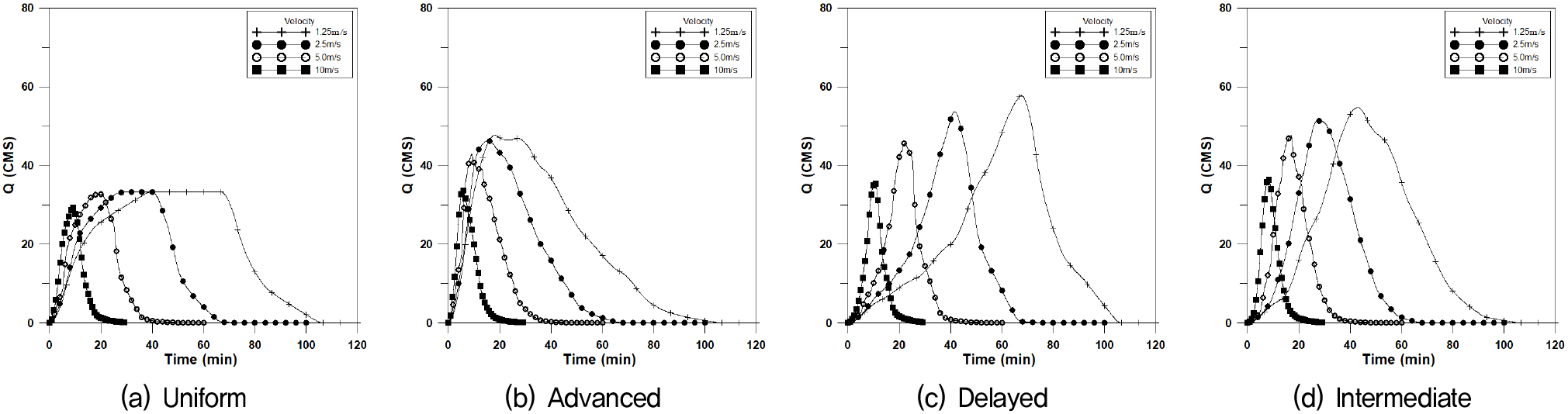
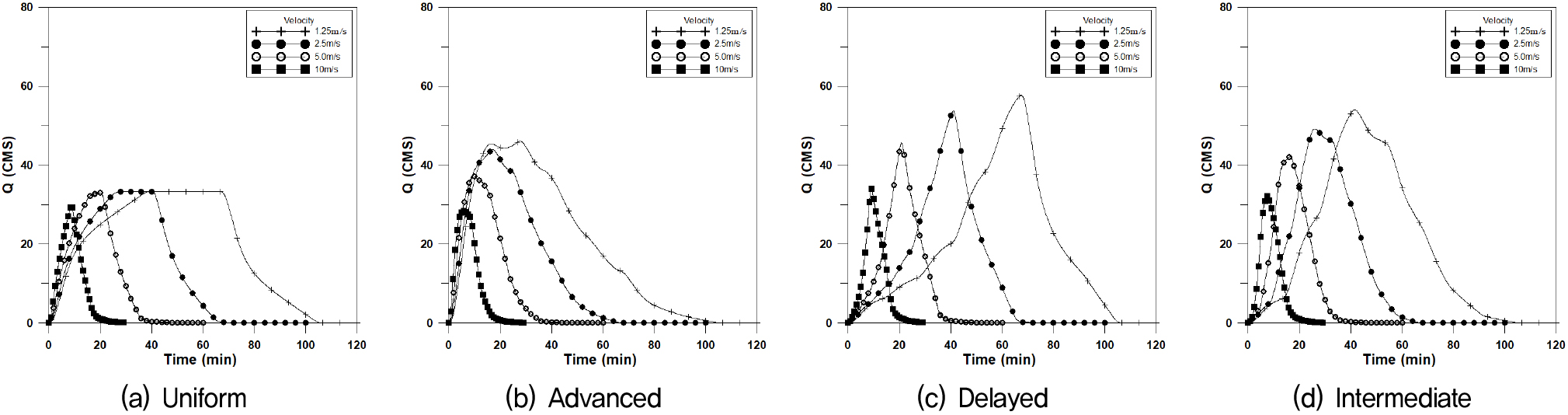
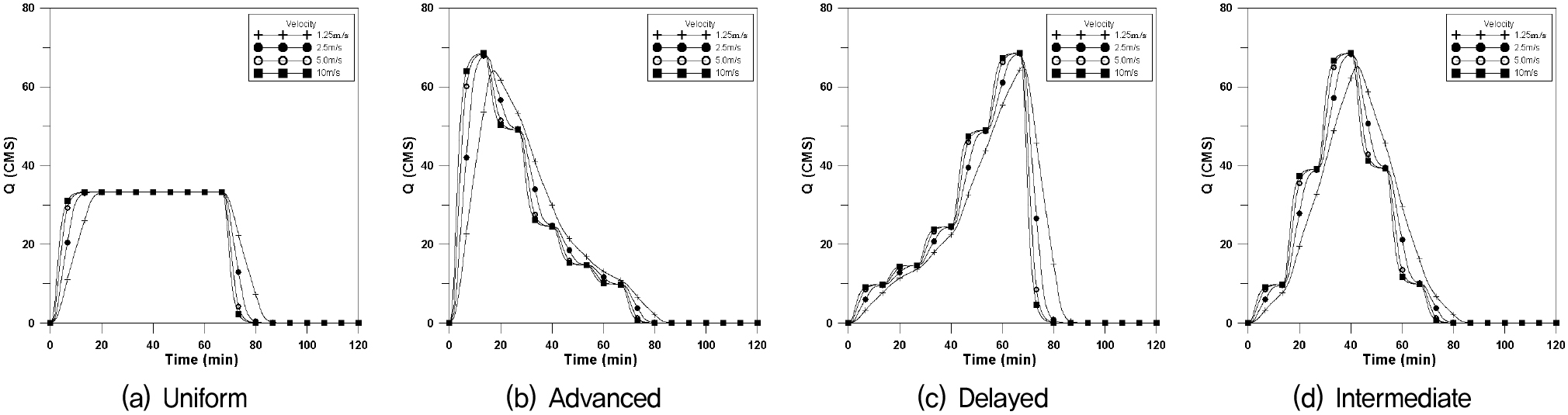
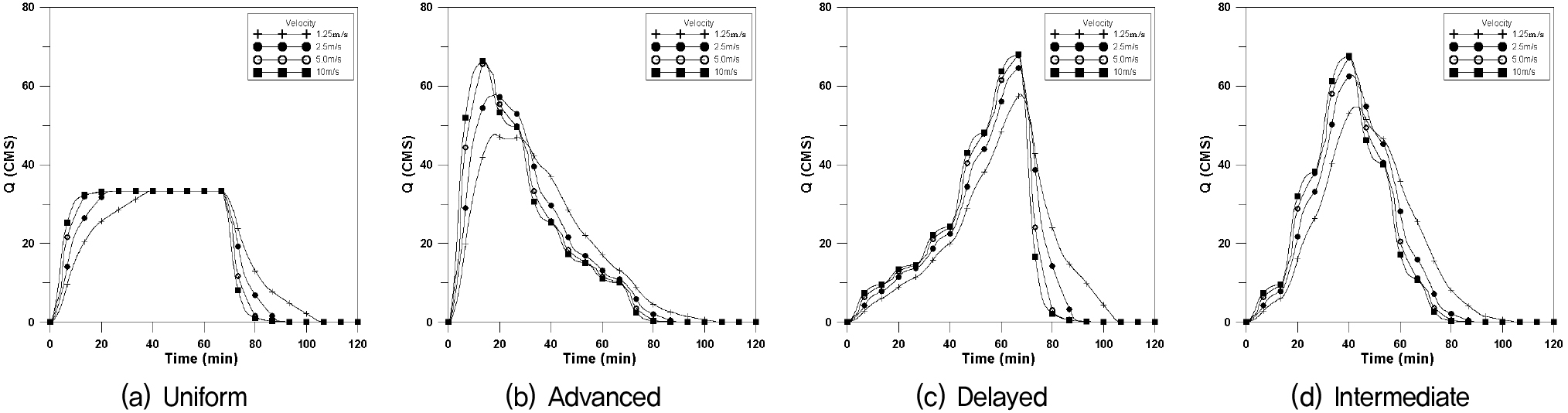
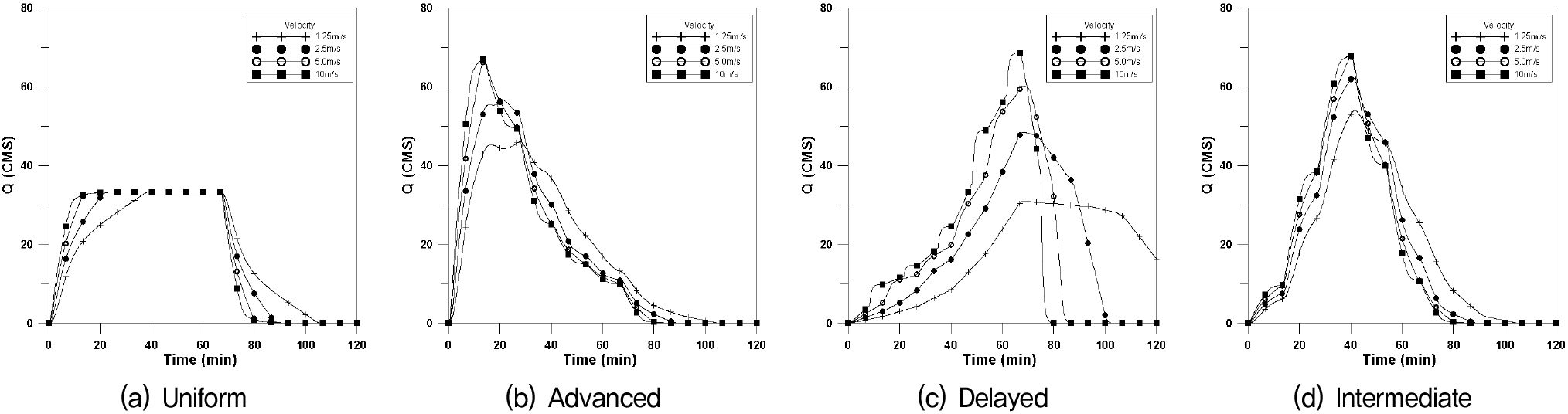
도달시간이 장방형유역에 비하여 길어지여 첨두유량이 일어나는 시간이 길어지고 첨두유량이 작아지는 경향을 보이는 유역형태이다. 본 연구에서는 폭 400m×길이 25,000m (F=0.16)인 신장형유역에 대하여 4개의 강우이동속도에 대하여 Fig. 12는 횡방향에 대한 수문곡선이며, Fig. 13은 하류방향, Fig. 14는 상류방향, Fig. 15는 대각선방향에 대한 수문곡선을 나타내었으며, 이에 대한 첨두유량과 첨두시간은 Table 5와 같이 나타내었다.
Table 5.
Peak discharge and peak time in a elongated basin (Equal rainfall at equal rainfall length)
신장형의 경우에도 균등분포형의 경우 첨두유량은 거의 같은 값을 나타내고 있으나 이동속도가 매우 빠른 10.0m/s 인 경우 이동강우 방향에 따라 첨두유량의 차이가 발생하고 있다. 이동속도가 느린 경우 중앙집중형 강우분포에서 하류방향의 지체시간이 매우 길어지는 것을 알 수 있으며, 이는 유역길이가 긴 신장형의 특징으로 강우분포가 유역전반에 걸쳐 영향을 미친다는 것을 의미한다.
4.4 강우강도와 총 강우량이 동일한 경우 정방형 유역에서의 유출분석
4.1~4.3에서 강우강도와 강우길이를 같게 놓고 분석하였는바 강우강도와 강우길이가 변하는 경우를 비교하기 위해 본 절에서는 강우강도와 총 강우량을 일정하다고(26,666.67m3) 가정하고 강우이동속도는 변하더라로 강우강도와 총 유출량은 변하지 않고 강우길이가 유출에 미치는 영향을 분석하고자 하였다. 강우이동속도에 대한 총 강우량을 일정하게 유지하기 위하여 강우강도를 일정(120mm/hr)하게 두고 강우길이를 변화시켜 유출을 비교하였다. 이 경우 동일한 총 강우량을 유지하기 위해 모든 이동방향에서 강우길이는 강우이동속도에 비례하여 변하는 것으로 가정하였다.
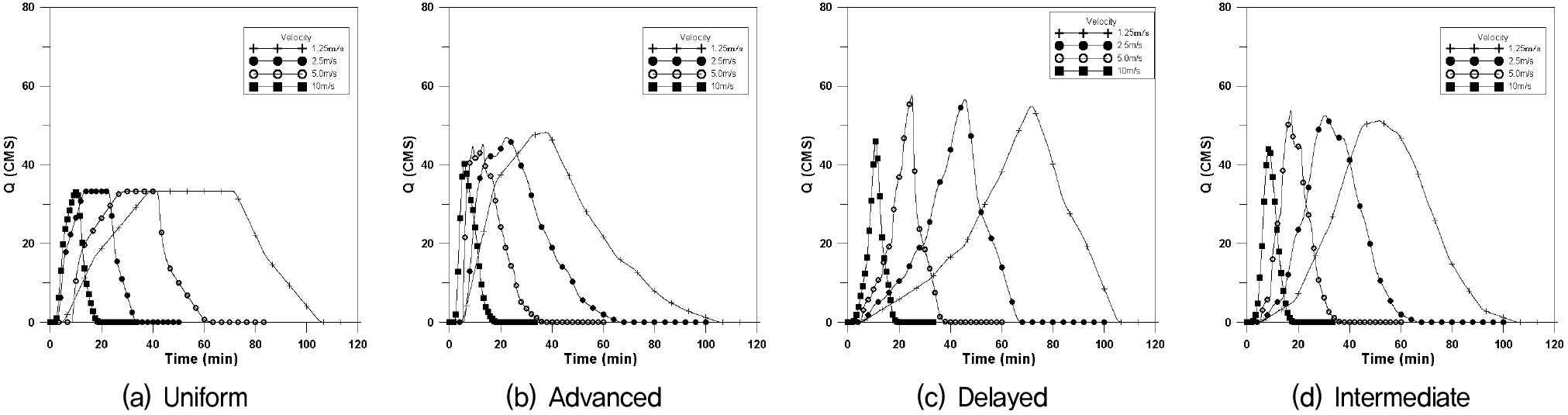
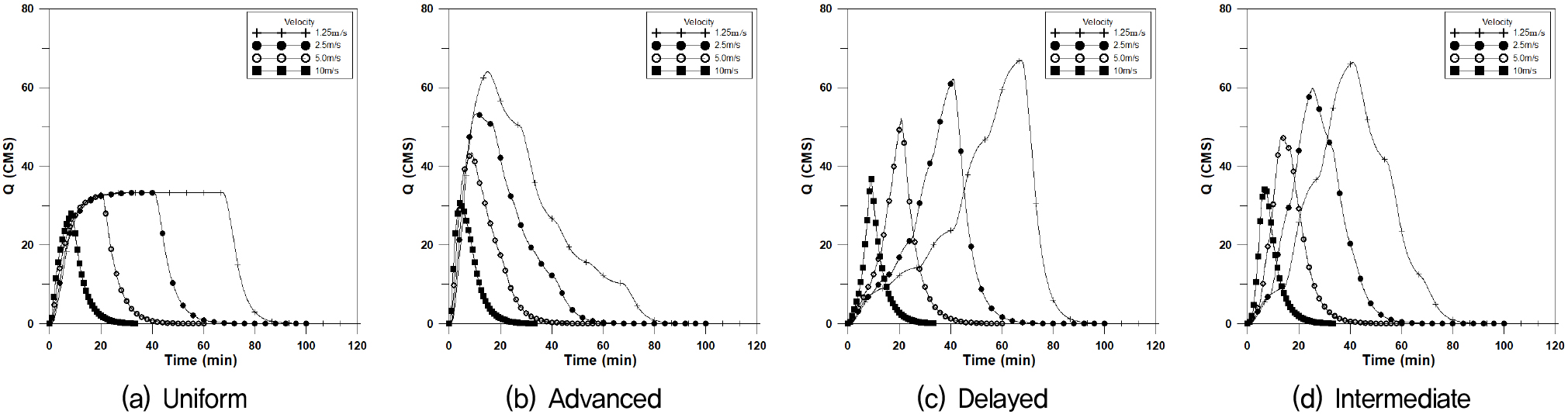
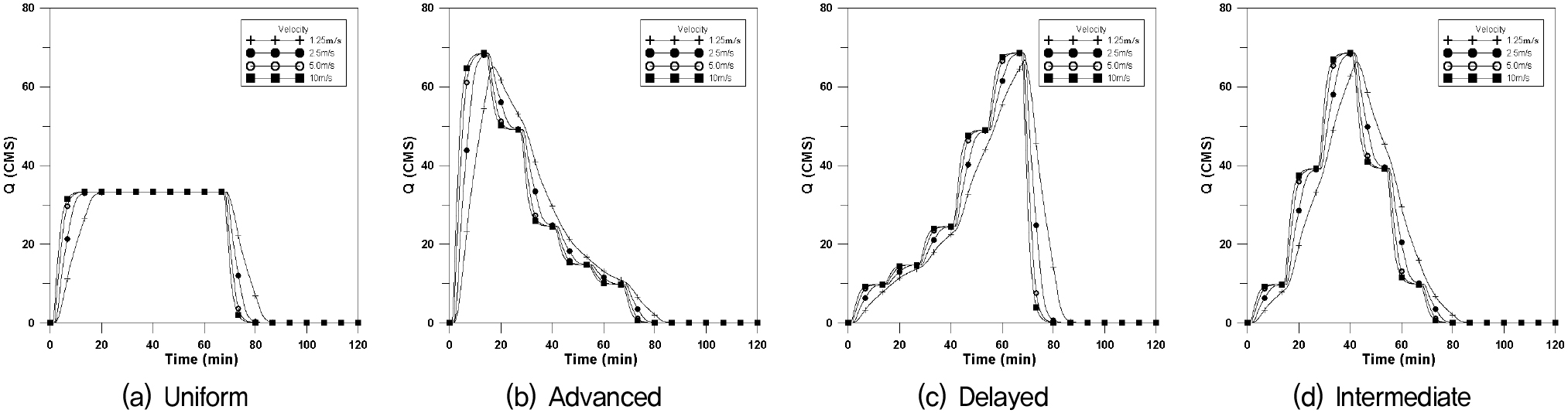
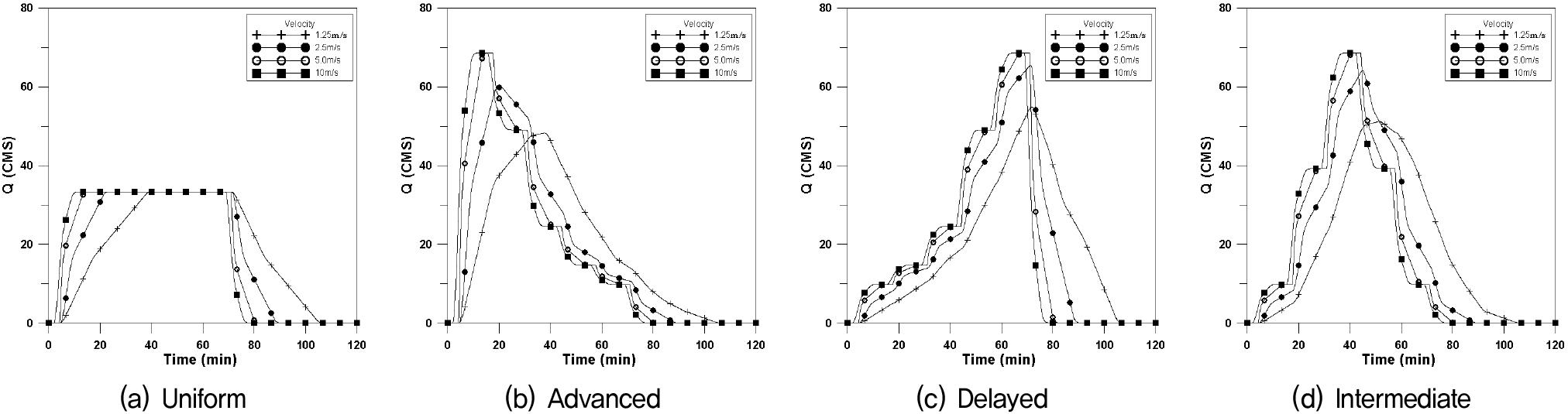
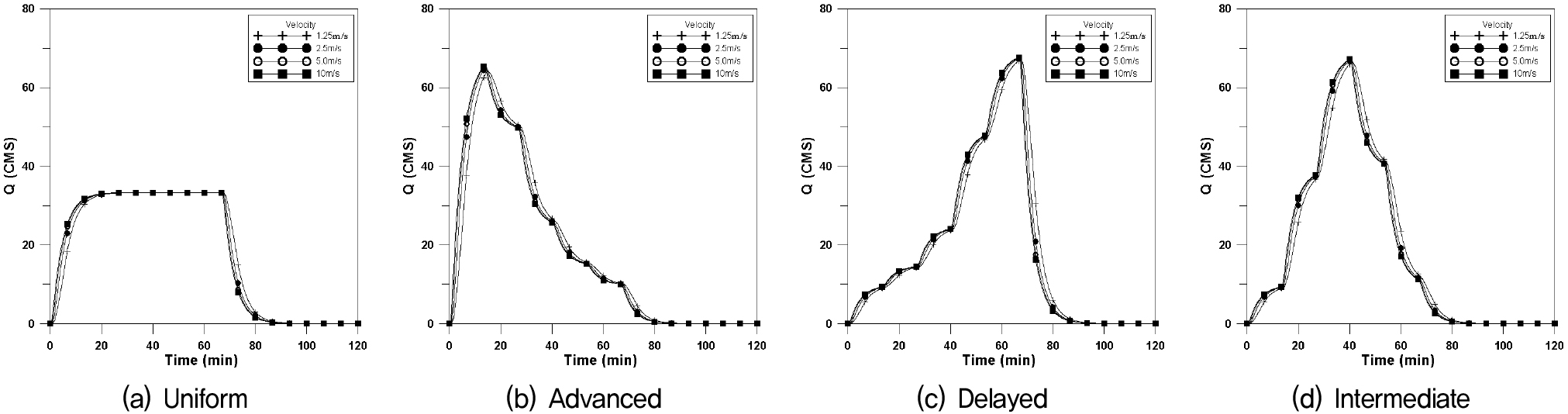
Fig. 16은 횡방향이동강우에 대하여 Fig. 17은 하류방향, Fig. 18은 상류방향, Fig. 19는 대각선방향에 대하여 4개의 강우이동속도에 대한 수문곡선을 나타내었으며, 이에 대한 첨두유량과 첨두시간은 Table 6과 같다.
Table 6.
Peak discharge and peak time in a square basin (Equal rainfall at various rainfall length)
정방형에서는 강우강도와 유출량이 같고 강우길이가 이동속도에 비례하게 영향을 준다고 가정한 경우 균등분포의 경우 첨두유량이 동일하게 나타나고 있으며, 전진형의 경우 상류방향으로의 유량이 작게 나타나고, 지연형의 경우 그 차이가 발생하지 않는다. 중앙집중형의 경우도 전진형과 같이 상류방향으로의 첨두유량이 작게 나타나고 있다. 첨두시간의 경우 지형학적 특징으로 인한 차이만 발생하였으며, 미세하게 지연형에서 첨두유량이 크게 나타나고 있다.
4.5 강우강도와 총 강우량이 동일한 경우 장방형 유역에서의 유출분석
4.4절 장방형의 경우와 같이 강우강도와 총 강우량을 일정하다고(26,666.67m3) 가정하고 장방형유역에서도 총 유출량은 변하지 않고 강우길이가 유출에 미치는 영향을 분석하고자 하였다. 강우강도를 일정(120mm/hr)하게 두고 강우길이를 강우이동속도에 비례시켜 분석하였다.
Fig. 20은 횡방향, Fig. 21은 하류방향, Fig. 22는 상류방향, Fig. 23은 대각선방향 등 4개의 강우이동속도에 대한 이동방향의 수문곡선을 나타내었으며, 이에 대한 첨두유량과 첨두시간은 Table 7과 같다.
Table 7.
Peak discharge and peak time in a oblong basin (Equal rainfall at various rainfall length)
장방형의 경우도 강우강도와 유출량이 같고 강우길이가 이동속도에 비례하게 영향을 준다고 가정한 경우 균등분포를 제외하고 모든 강우분포형에서 첨두유량은 거의 비슷하게 나타났으며, 분포형의 특징으로 인한 첨두시간의 차이만 발생하였다. 이동속도가 10.0m/s인 경우 횡방향에서 균등분포형을 제외하고 모든 강우분포형에서 첨두유량이 같게 나타났다.
4.6 강우강도와 총 강우량이 동일한 경우 신장형 유역에서의 유출분석
정방형, 장방형의 경우와 같이 강우강도와 총 강우량을 일정하다고(26,666.67m3) 가정하고 신장형유역에서도 총 유출량은 변하지 않고 강우길이가 유출에 미치는 영향을 분석하고자 하였다. 강우강도를 일정(120mm/hr)하게 두고 강우길이를 강우이동속도에 비례시켜 분석하였다.
Fig. 24는 횡방향, Fig. 25는 하류방향, Fig. 26은 상류방향, Fig. 27은 대각선방향이며, 4개의 강우이동속도에 대한 이동방향의 수문곡선을 나타내었으며, 이에 대한 첨두유량과 첨두시간은 Table 8과 같다.
Table 8.
Peak discharge and peak time in a elongated basin (Equal rainfall at various rainfall length)
신장형의 경우 전진형, 지연형, 중앙집중형 강우분포형에서 첨두유량은 거의 비슷하게 나타났으며, 분포형의 특징으로 인한 첨두시간의 차이만 발생하였다. 이동속도가 5.0m/s, 10.0m/s인 경우 하류방향에서 강우분포형에 관계없이 첨두유량이 같게 나타났다.
5. 결 론
본 연구는 이동강우의 특성을 규명하고자 유역형상을 정방형, 장방형, 신장형 3가지 형태의 모형유역으로 정하였고, 이동강우속도를 1.25m/s, 2.5m/s, 5.0m/s, 10.0m/s 등으로 구분하여 각 이동속도별 이동방향을 횡방향, 하류방향, 상류방향, 대각선방향 4가지 방향에 대하여 구분하였다. 모형유역의 방향과 강우의 이동방향과의 관계에 따라 유역모형에 내린 강우량에 영향이 발생하며, 강우의 이동방향에 따라 수문곡선의 모양이 달라지는 것을 알 수 있다. 기존의 연구에서는 유역의 모양이 작고 이동방향을 3가지로 분석하였으나, 본 연구에서는 유역의 크기를 향후 실제 소유역에서의 유출형태와 비교하기 위해 1km2(1,000,000m2)으로 정하였으며, 강우이동방향도 대각선방향을 추가하여 분석하였다.
강우이동방향이 유역 상류에서 하류로 이동하면 상류에서 발생한 유량이 하류에서 발생하는 유량과 중첩되면서 유량이 증가하게 되며, 하류에서 상류로 이동 시에는 상류에서 발생한 강우가 하류에 도달할 시점에는 하류에서 발생한 유량은 이미 유역 출구점을 빠져나가게 되어 홍수량이 작아지는 것을 알 수 있다. 대각선방향의 경우 상류방향과 횡방향의 중간 정도의 첨두유량을 보이고 있다. 이는 방향성이 유출에 영향이 있는 것을 보여준다.
유출분석 시 운동파이론 및 연속방정식을 이용하여 이동강우와 유출의 영향을 분석하였으며, 강우분포형은 균등분포, 전진형, 지연형, 중앙집중형을 사용하였다. 3가지 유역모양과 4개의 이동속도, 4개의 강우분포형, 4개의 이동방향을 사용하여 유출을 분석한 결과 다음과 같은 결론을 얻을 수 있다.
첫째, 첨두유량, 첨두시간은 유역의 모양, 이동속도, 강우분포형 등에 영향을 받는 것을 알 수 있고, 이를 나타내기 위해 강우강도와 강우길이가 동일한 경우와 강우강도와 총 강우량이 동일한 경우로 나누어 분석하였고, 수문곡선의 양상은 두 경우 비슷한 것으로 나타났다.
둘째, 장방형유역의 경우 상류방향과 신장형유역의 횡방향 이동강우에서는 강우이동속도에 영향을 받지 않고 수문곡선이 중첩되는 것을 알 수 있다. 이는 유역의 모양에 영향을 받아 나타나는 것임을 알 수 있다.
셋째, 이동속도에 따르는 수문곡선의 변화를 비교해 보면 상류방향과 하류방향에서는 신장형유역에서의 변화가 매우 크게 나타났으며, 장방형의 경우 변화가 크지 않는 것으로 나타났다.
넷째, 강우강도와 강우길이가 동일한 경우에는 균등분포형의 경우 정방형에서는 첨두유량이 거의 같게 나타났으나, 장방형과 신장형에서는 이동속도가 빠른 경우 첨두유량이 점차 작아지고 전진형의 경우는 이동속도가 커질수록 첨두유량의 감소폭이 제일 크게 나타나고 있다. 지연형의 경우 균등분포형을 제외하고는 첨두유량의 감소폭이 작고 첨두유량의 크기는 제일 크게 발생하는 것을 알 수 있다. 중앙집중형의 경우 지연형과 전진형의 중간형태로 나타난다.
다섯째, 강우이동속도에 관계 없이 하류방향의 첨두유량이 상류방향의 첨두유량보다 크게 나타나고 있으며, 균등분포형의 경우 이동속도가 매우 빠른 경우를 제외하고는 거의 비슷하게 나타나고 있다.
본 연구를 통하여 유역의 형상과 이동속도, 강우분포형에 따른 유출의 양상을 모형을 통하여 규명하였고, 대칭성을 가지고 있는 소유역을 정하여 근래 발생한 집중호우에 따른 실제 유출과의 비교를 실시하여 실제유역에서의 유출특성을 알 수 있을 것으로 예측된다.