Study of Prediction of Liquefaction Potential Index Based on Machine Learning Method

Junseo Jeon; Jongkwan Kim; Jintae Han; Seunghwan Seo; Byeonghan Jeon

doi:10.14481/jkges.2024.25.11.5

Preview

Journal of the Korean Geo-Environmental Society. 1 November 2024. 5-12
https://doi.org/10.14481/jkges.2024.25.11.5

Study of Prediction of Liquefaction Potential Index Based on Machine Learning Method

기계학습기법을 통한 액상화 발생가능 지수 예측에 관한 연구

Junseo Jeon¹

Jongkwan Kim²^*

Jintae Han³

Seunghwan Seo⁴

Byeonghan Jeon⁵

전 준서¹

김 종관²^*

한 진태³

서 승환⁴

전 병한⁵

¹Senior Researcher, Department of Geotechnical Engineering Research, Korea Institute of Civil Engineering and Building Technology (KICT)

²Senior Researcher, Department of Geotechnical Engineering Research, Korea Institute of Civil Engineering and Building Technology (KICT)

³Research Fellow, Department of Geotechnical Engineering Research, Korea Institute of Civil Engineering and Building Technology (KICT)

⁴Senior Researcher, Department of Geotechnical Engineering Research, Korea Institute of Civil Engineering and Building Technology (KICT)

⁵Manager, Institute of Technology, LT SAMBO

^{*Corresponding Author}

License (open-access, http://creativecommons.org/licenses/by-nc/4.0/):

It is identical to Creative Commons Non-Commercial Licence.

ABSTRACT

In this study, the liquefaction potential index was assessed using actual borehole data and seismic waves, and a predictive model was developed based on machine learning methods. A total of 10 features were selected including factors reflecting the characteristics of the seismic waves. To identify candidate methods, a preliminary test was conducted using commonly used machine learning methods for regression, followed by Bayesian optimization to optimize the hyperparameters for these candidate methods. Among artificial neural networks, Gaussian process regression, and random forest, it was found that the random forest effectively predicted the liquefaction potential index, as indicated by a low root mean square error, a high coefficient of determination, and considerations regarding overfitting. However, it was noted that the model tends to underestimate the liquefaction potential index when the index was 5 or higher.

Keywords

Liquefaction potential index

Borehole data

Machine learning

Bayesian optimization

Hyperparameter

실제 시추공 정보 및 지진파를 이용하여 액상화 발생가능 지수를 산정하고, 기계학습기법을 이용하여 액상화 발생가능 지수 예측모델을 학습하였다. 학습을 위해 지진파의 특징을 반영한 인자를 포함하여 총 10가지의 특징을 선택하였다. 일반적으로 이용되는 기계학습기법 중 사전학습을 통해 후보 모델을 선정하고, 후보 모델에 대해 베이지안 최적화를 적용하여 초매개변수를 최적화시켰다. 인공신경망, 가우시안 프로세스 회귀, 랜덤 포레스트 중 평균제곱근오차, 결정계수 및 과대적합 여부를 종합한 결과, 랜덤 포레스트가 액상화 발생가능 지수를 잘 예측하였다. 다만, 액상화 발생가능 지수가 5 이상에서는 액상화 발생가능 지수를 과소예측하는 경향을 보였다.

키워드

액상화 발생가능 지수

시추공 자료

기계학습

베이지안 최적화

초매개변수

MAIN

1. 서 론
2. 방법론
2.1 자료 및 전처리
2.2 기계학습 모델 선정 및 초매개변수 최적화
3. 결 과
4. 결 론

1. 서 론

액상화는 지진 시 지반 및 시설물에 큰 피해를 유발한다. 1964년 니이가타 및 알래스카 지진에서 액상화가 처음 보고된 이래 1995년 고베 지진, 2011년 동일본 대지진, 크라이스트쳐치 지진 등 많은 지진에서 액상화 피해가 다수 보고되었다. 국내에서는 2017년 포항지진에서 계기지진 이래 최초로 액상화 현상이 목격되어, 국내에서도 충분히 액상화가 발생할 수 있음을 시사하였다. 이에 따라 국내에서도 액상화 발생 위험이 큰 지역을 사전에 선별하고, 이에 대한 대응책을 수립하기 위해 액상화 위험지도와 관련된 연구가 수행되기도 하였다.

액상화 발생 여부는 액상화 안전율로 평가한다. 액상화 안전율은 액상화에 대한 지반의 저항력을 나타내는 반복저항응력비(Cyclic Resistance Ratio, CRR)를 지진에 의한 외력을 나타내는 반복전단응력비(Cyclic Stress Ratio, CSR)로 나누어서 평가하며, 액상화 안전율이 1 이하이면 액상화가 발생한다고 평가한다. 반복전단응력비는 지표면 최대가속도를 바탕으로 응력감소계수를 사용하여 평가하는 방법과 지반응답해석을 통해 얻어진 각 층의 최대전단응력을 이용하여 평가하는 방법이 있다. 내진설계일반 KDS 17 10 00에서는 지반응답해석을 통해 얻어진 각 층의 최대전단응력을 통해 반복전단응력비를 산정하도록 제시하고 있다.

지반응답해석을 통해 액상화 평가를 수행하는 방법은 평가 대상 시추공의 개수가 적은 경우에는 큰 문제가 되지 않는다. 하지만, 앞서 언급한 바와 같이 액상화 위험지도 제작 등과 같이 구·시·도를 대상으로 액상화 평가를 수행할 경우 많은 시간이 소요된다. 예를 들어 서울시의 경우 40,000 여공이 넘는 시추공 자료가 존재하며, 이를 대상으로 다양한 지진 시나리오에 대해 평가할 경우 많은 시간이 소요된다. 따라서 이와 같은 방법은 지진 발생 전 소수의 지진 시나리오를 기반으로 한 액상화 위험도 평가에는 적합하나 다양한 지진 시나리오 또는 실제 지진발생 시 신속한 액상화 위험도를 통해 복구대응 등에 활용하기에는 적합하지 않다.

앞서 언급된 한계를 극복하기 위해 최근 기계학습 기반으로 한 예측방법에 많은 연구가 수행되고 있다.

기계학습을 통한 액상화 평가는 인공신경망을 이용한 Goh(1994)의 연구로 시작되었다. 초기 인공신경망(Artificial Neural Network, ANN)(Goh, 1994; Juang et al., 2003)을 시작으로 유전자알고리즘(Genetic Algorithm, GA)(Fattah et al., 2002; Baziar et al., 2011; Sabbar et al., 2019), 서포트벡터머신(Support Vector Machine, SVM)(Pal, 2006; Goh & Goh, 2007)이 이용되었고, Chern et al.(2008)부터 시작하여 최적화 알고리즘 및 특징공학(Feature engineering) 기술이 적용된 하이브리드-기계학습 방법이 많이 이용되고 있다(Jas & Dodagoudar, 2023). 액상화 평가에 있어 최종 예측 목표(예를 들어 액상화 발생여부, 액상화 발생가능 지수 예측 등), 고려 인자의 종류 및 형태에 따라 적합한 기계학습 기법이 달라진다. 본 연구에서는 적용이 쉬운 단일 기계학습 모델을 대상으로 한정하였다. Ghani et al.(2024)에 따르면, 인공신경망(ANN)과 앙상블(Ensemble) 기반 기계학습이 다른 학습모델에 비해 많이 액상화 예측에 사용되어 왔다. Ozsagir et al.(2022)은 세립분 지반의 액상화 예측을 위해 인공신경망과 의사결정트리(Decision Tree, DT)를 포함한 기계학습을 적용하여, 의사결정트리가 90% 이상의 정확도를 가짐을 확인하였다. Sabbar et al.(2019)은 인공신경망(ANN)과 유전자알고리즘(GP) 중 인공신경망 모델이 유전자알고리즘보다 더욱 액상화 예측에 있어 높은 정확도를 보임을 확인하엿다. Kohestani et al.(2015)는 226개의 현장 콘관입치값(CPT값)을 이용하여 액상화 발생여부를 예측하였다. 랜덤 포레스트(Random Forest, RF)가 서포트벡터머신(SVM), 인공신경망(ANN)보다 더욱 예측을 잘하는 것을 확인하였다. Samui & Sitharam(2011)은 인공신경망(ANN)과 서포트벡터머신(SVM)을 이용하여 표준관입시험값(SPT-N)과 반복전단응력비 자료를 통해 액상화 발생여부를 예측하였고, 예측모델을 표준관입시험값(SPT-N)과 지표면 최대가속도를 이용하여 단순화하는 시도를 하였다. 이 경우, 인공신경망(ANN)보다 서포트벡터머신(SVM)이 액상화 발생여부를 더 정확하게 예측함을 보였다. 국내에서는 Baek & Choi(2019)가 실시간 예측 가능한 액상화 위험지도 작성을 위해 수도권지역의 시추공 자료를 이용하여 액상화 발생가능 지수를 계산하고, 지진가속도와 상관관계 분석을 통해 로그함수 형태의 관계식을 제안하였다. 다만 관계식이 지역적 한계성을 내포하고 있어 보완 필요성을 언급하였다.

본 연구에서는 먼저 총 13,236개소의 시추공 자료 및 21개의 지진파(7개의 지진파 및 3개의 재현주기)를 이용하여 액상화 발생가능 지수를 계산하였다. 이후 그 결과를 바탕으로 일반적으로 사용되는 기계학습기법을 통해 후보 학습기법을 선정하고, 후보 학습기법을 대상으로 초매개변수 최적화를 통해 최종 액상화 발생가능 지수 예측모델을 구축하였다.

2. 방법론

2.1 자료 및 전처리

액상화 발생가능 지수(Liquefaction Potential Index, LPI)는 Iwasaki et al.(1978)에 의해 Eq. (1)과 같이 제안되었고, 액상화 안전율에 심도에 따른 가중치를 곱하고 적분한 형태로 표현된다.

(1)

L P I = \int_{0}^{20} F (z) w (z) d z

여기서, $F (z) = 1 - F s (z)$ , $w (z) = 10 - 0.5 z$ , $F s$ =액상화 안전율, $z$ =심도

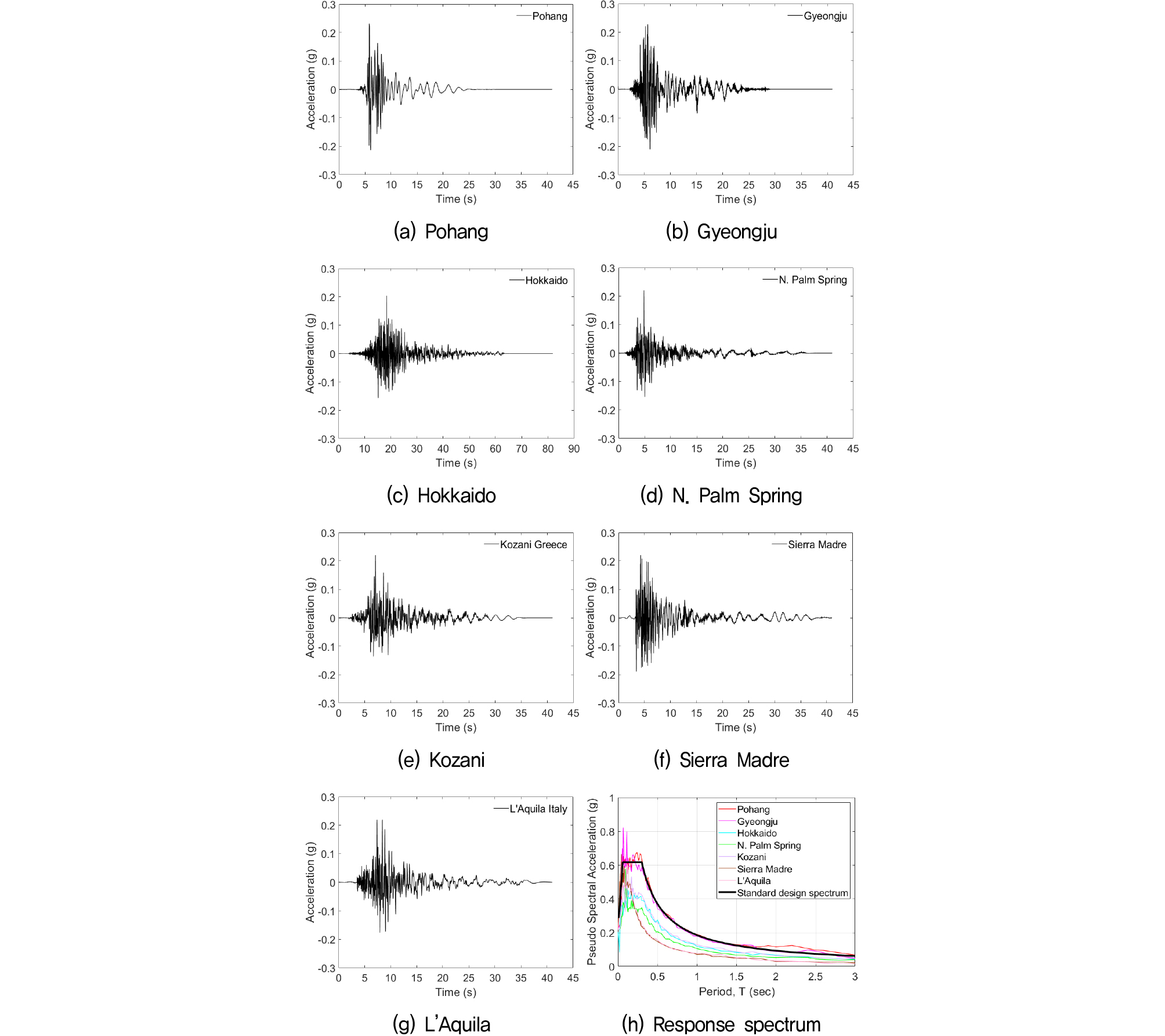
액상화 발생가능 지수(LPI)를 계산하기 위해, 국토지반정보 포털시스템에서 제공받은 서울특별시의 24,327공의 지반정보 중 액상화 평가가 가능한 13,236공의 시추공 자료를 수집하였다. 액상화 평가에 활용된 지진목록은 Table 1과 같으며, 각 지진파의 가속도-시간이력은 Fig. 1과 같다. 본 연구에서는 Table 1과 같이 총 7개의 지진파를 바탕으로 내진설계기준 공통적용사항에서 제시하는 기준에 따라 재현주기(500, 1,000, 2,400년)별 표준설계스펙트럼에 부합하도록 스펙트럼 매칭을 수행하였다. 다만 액상화 평가에서는 최대가속도가 중요한 인자이므로 최대가속도를 맞추는 것을 우선시하였다. 그 결과 각 재현주기별 7개씩 총 21개의 지진파를 활용하였다.

https://cdn.apub.kr/journalsite/sites/jkges/2024-025-11/N0480251101/images/kges_25_11_01_F1.jpg

Fig. 1

Horizontal acceleration seismic waves matched with a return period of 2,400 years

Table 1.

Earthquake information considered in this study

Earthquake	Country	Year	Magnitude (M)	Distance (km)	PGA (g)	Mean Period sec)
Pohang	Korea	2017	5.4	9.5	0.27	0.48
Gyeongju	Korea	2016	5.8	9.1	0.41	0.15
Hokkaido	Japan	2018	6.7	26	0.17	0.52
N. Palm Spring	USA	1986	6.06	16.55	0.13	0.15
Kozani	Greece	1995	6.4	14.13	0.21	0.28
Sierra Madre	USA	1991	5.61	10.36	0.28	0.25
L’Aquila	Italy	2009	5.6	14.95	0.14	0.32

먼저 학습데이터를 생성하기 위해 13,236공의 시추공을 대상으로 각각 총 21개의 지진파에 대한 지반응답해석을 수행하였다. 지반응답해석을 통해 얻어진 각 층의 최대전단응력을 활용하여 KDS 17 10 00 내진설계일반에 따라 액상화 안전율을 산출하였으며, 이를 바탕으로 Eq. (1)를 통해 액상화 발생가능 지수(LPI)를 계산하였다. 그 결과 총 277,956개의 액상화 발생가능 지수(LPI)를 산출하였다. 그 중 액상화 발생가능 지수(LPI)가 0인 경우는 89.3%인 248,207개, 0보다 큰 경우는 10.7%인 29,749개였다. 만약 불균형이 큰 해당 자료를 그대로 기계학습에 이용할 경우, 액상화 발생가능 지수(LPI)가 0을 예측하도록 집중학습되는 등 과대적합 가능성이 높다.

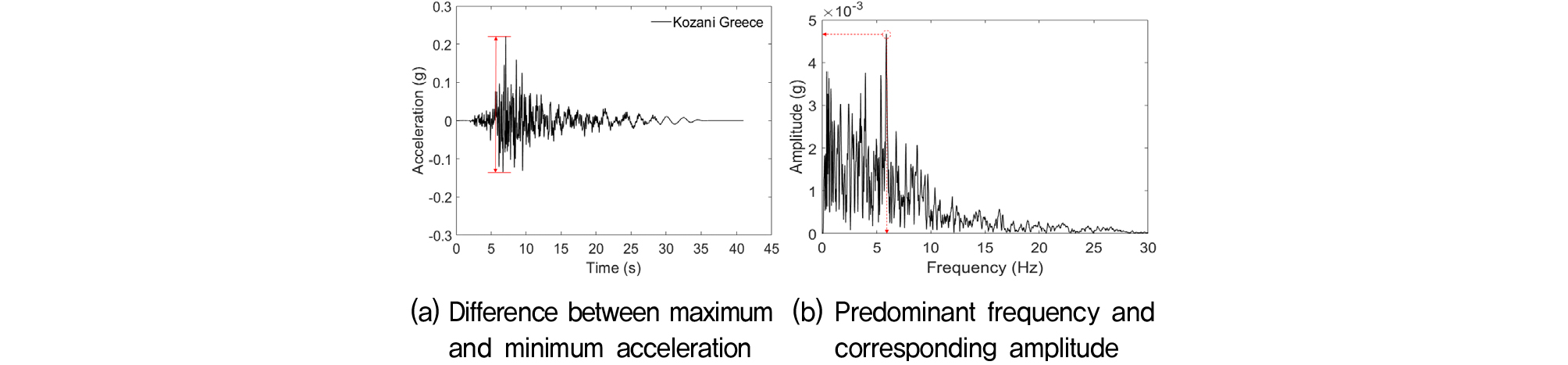
이를 해결하기 위해 액상화 발생가능 지수(LPI)가 0 이상인 자료 22,974개와 동일하게 액상화 발생가능 지수(LPI)가 0인 자료에서 무작위로 22,974개를 선정하였다. 지진파 가속도-시간이력의 시계열 자료를 그대로 이용하지 않고 일부 특징을 이용하였다. 사용된 지진파 특성은 Fig. 2와 같이 가속도-시간이력에서 전 시간에 대해 최대가속도와 최소가속도의 차, 고속 퓨리에 변환(Fast Fourier Transform, FFT)을 통해 주파수 이력에서 우세주파수(Predominant frequency)와 이에 해당하는 진폭(Amplitude)를 이용하였다. 시추공의 정보는 표준관입시험값(SPT-N), 단위중량, 세립분함량(%), 유효연직응력(층 경계, 층 중간), 종료심도, 지하수위를 이용하였다. 각 시추공 조사자료의 경우에는 다양한 지층이 분포되어 있고, 각 지층의 두께 및 지하수위는 상이하다.

https://cdn.apub.kr/journalsite/sites/jkges/2024-025-11/N0480251101/images/kges_25_11_01_F2.jpg

Fig. 2

Considered features obtained from the earthquake record

각 특징(Feature)을 고려할 때 심도별 자료를 전부 입력하는 대신 대푯값을 이용하였다. 본 연구에서는 각 지층 두께를 가중치로 가정하여 각 특징에 곱한 후 조사 종료심도로 나눈 평균값을 이용하였다. 예를 들어 3개의 지층, 1번째 지층이 2m 두께, SPT-N 30, 2번째 지층이 3m 두께, SPT-N 35, 3번째 지층이 5m 두께, SPT-N 40 일 경우, 해당 시추공의 SPT-N는 (2×30+3×35+5×40)/(2+3+5)=36.5를 대푯값으로 산정하였다. Table 2는 최종적으로 액상화 발생가능 지수를 예측함에 있어 기계학습에 사용된 특징을 나타낸다.

Table 2.

Considered features for LPI prediction

No	Feature	Unit
1	SPT-N	-
2	Unit weight	t/m³
3	Fine content	%
4	Effective vertical overburden stress at the center of layer	kPa
5	Effective vertical overburden stress at layer interface	kPa
6	Depth	m
7	Water table	m
8	Acceleration difference between maximum and minimum value	g
9	Predominant frequency	Hz
10	Amplitude at predominant frequency	g

2.2 기계학습 모델 선정 및 초매개변수 최적화

본 연구에서 Mathwork사의 MATLAB 프로그램을 이용하여 액상화 발생가능 지수를 기계학습 기반으로 예측하였다. 먼저 사전학습으로 다양한 분류 방법에 대해 액상화 발생가능 지수 예측에 적합한 방법을 비교·선정하였으며, 선택된 방법에 대해 초매개변수 최적화를 수행하여 예측모델을 학습하였다. 학습자료(Training data)와 시험자료(Test data)를 8:2의 비율로 나누고, 학습자료에 대해 5겹 교차검증을 수행하였다. 학습자료를 동일한 크기로 5개 부분으로 나누고, 이 중 4개 부분은 학습에 이용하며, 나머지 1개 부분은 검증에 이용된다. 사전학습에 고려한 예측 방법, 구조 및 결과는 Table 3과 같다.

Table 3.

Results of selecting appropriate ML model for LPI prediction

Model	Structure		RMSE
Linear Regression	with linear term only		3.7648
	with interactions linear		3.3323
	with robust linear		5.6465
	with stepwise linear		3.3334
Decision Tree (DT)	with minimum leaf size of 4		2.2727
	with minimum leaf size of 12		2.6605
	with minimum leaf size of 36		2.8796
Support Vector Machine (SVM)	with linear kernel		4.2111
	with quadratic kernel		3.5058
	with cubic kernel		14.081
	with Gaussian kernel scale of 0.79		3.1066
	with Gaussian kernel scale of 3.2		3.1985
	with Gaussian kernel scale of 13		3.5334
Ensemble	Boosted	with minimum leaf size of 8 and learning rate of 0.1	3.0643
	Bagged	with minimum leaf size of 8	2.0893
Gaussian Process Regression (GPR)	with squared exponential kernel		3.062
	with Matern 5/2 kernel		3.0324
	with exponential kernel		2.9537
	with rational quadratic kernel		3.0318
Neural Network (NN)	with fully connected layer of 1 having layer size of 10		3.0097
	with fully connected layer of 1 having layer size of 25		2.8951
	with fully connected layer of 1 having layer size of 100		2.7245
	with fully connected layer of 2 having each layer size of 10		2.8627
	with fully connected layer of 3 having each layer size of 10		2.8418
	with SVM learner		3.9917
	with least squares kernel		3.6946

사전학습 결과, 앙상블(최소 2.0893), 신경망(최소 2.7245), 가우시안 프로세스 회귀(최소 2.9537)순으로 낮은 평균제곱근오차(RMSE)를 보였다. 본 연구에서는 사전학습 결과를 토대로 배깅 기반 앙상블, 인공신경망, 지수커널을 이용한 가우시안 프로세스 회귀로 한정하여 초매개변수 최적화를 수행하였다. 과대적합(Overfitting)을 방지하기 위해 특징(Feature)을 임의로 선택하여 여러 개의 의사결정 트리를 생성하고, 각 의사결정 트리의 결과를 바탕으로 최종 결과를 도출하는 랜덤 포레스트(RF)를 앙상블 모델로 이용하였다. 신경망 학습에서는 과대적합 방지를 위해 L2 정규화(Ridge regularization)를 고려한 훈련 성능평가, 검증 세트의 평균제곱오차가 감소하다 다시 증가할 때 훈련을 중지시키는 조기 종료(Early stopping)를 적용하였다. 조기 종료 조건으로 검증 세트의 평균제곱오차가 1e-6 이하면 학습을 중지하였다. 또한 평균제곱오차가 감소하다 다시 증가할 때 훈련을 바로 중지하지 않고, 20번의 에포크(Epoch) 동안 평균제곱오차의 변화량이 감소하지 않을 때 훈련을 중지하도록 설정하였다.

초매개변수의 최적화를 위해서 본 연구에서는 베이지안 최적화를 이용하였다. 초매개변수 최적화는 사람의 직관이나 경험에 기반하여 찾는 매뉴얼 탐색(Manual search), 파라미터의 탐색 구간을 정하고 일정한 간격을 두고 선정하여 성능을 확인하는 그리드 탐색(Grid search), 탐색 구간 내에서 무작위로 선정하여 성능을 확인하는 무작위 탐색(Random search), 두 확률 변수의 사전 확률과 사후 확률 사이의 관계를 나타내는 베이즈 정리(Bayes’ theorem)를 기반으로 하여 미지의 목적함수를 최대화하는 해를 찾는 베이지안 최적화(Bayesian optimization)가 이용된다. 그리드 탐색(Grid search)와 무작위 탐색(Random search)은 다음 초매개변수 선정과정에서 이전까지 조사한 초매개변수들의 성능을 고려하지 않는 반면, 베이지안 최적화는 사전지식을 반영하면서 탐색을 수행하는 이점으로 많이 이용되고 있다.

베이지안 최적화(Bayesian optimization)는 대체모델(Surrogate model)과 획득함수(Acquisition function)로 구성된다. 대체모델은 실제 목적함수를 추정하는 모델로써 획득 함수로부터 구한 다음 탐색값을 기반으로 모델을 개선하는 역할을 하며, 획득함수는 앞서 개선된 대체 모델을 바탕으로 착취(Exploitation)와 탐색(Exploration) 과정을 통해 다음 입력값을 결정하는 역할을 한다. 본 연구에서는 대체모델로 가우시안 프로세스 회귀(Gaussian Process Regression)를 사용하였고, 이때 사용된 커널(Kernel)은 ARD matern 5/2 kernel를 이용하였다. 또한 획득함수로는 최대 예상 향상도(Expected Improvement)를 이용하였다.

Table 4는 본 연구에서 고려한 인공신경망, 가우시안 프로세스 회귀, 랜덤 포레스트의 초매개변수, 범위 및 최적화 결과를 나타낸다. 모델의 평가지표로는 결정계수, 평균제곱근오차를 이용하였다. 결정계수를 통해 예측값과 목표값의 정확도(Accuracy)를 비교하였으며, 평균제곱근오차를 통해 모델 정밀도(Precision)를 분석하였다.

Table 4.

Results of hyperparameter optimization

Method	Hyperparameter	Considered range	Optimization result
Neural Network (NN)	Number of layers	1~5	3
	Activation function	relu, tanh, sigmoid	sigmoid
	λ (L2 regulation)	2.7205e-10~2.7205	2.5644e-05
	Layer size	10~100	1st layer: 100 2nd layer: 22 3th layer: 3
Gaussian Process Regression with exponential kernel (GPR)	Sigma	1.e-4~48.0670	4.1128e-4
	Basis function	constant, none, linear, pure quadratic	linear
	Kernel scale	41.38~41380	40922
Random Forest (RF)	Maximal number of branch node splits	1~30,000	3397
	Number of least observation needed at each leaf	1~20	5
	Number of predictor variables (randomly selected) for each decision split	1~9	9
	Number of learning cycles	10~500	414

3. 결 과

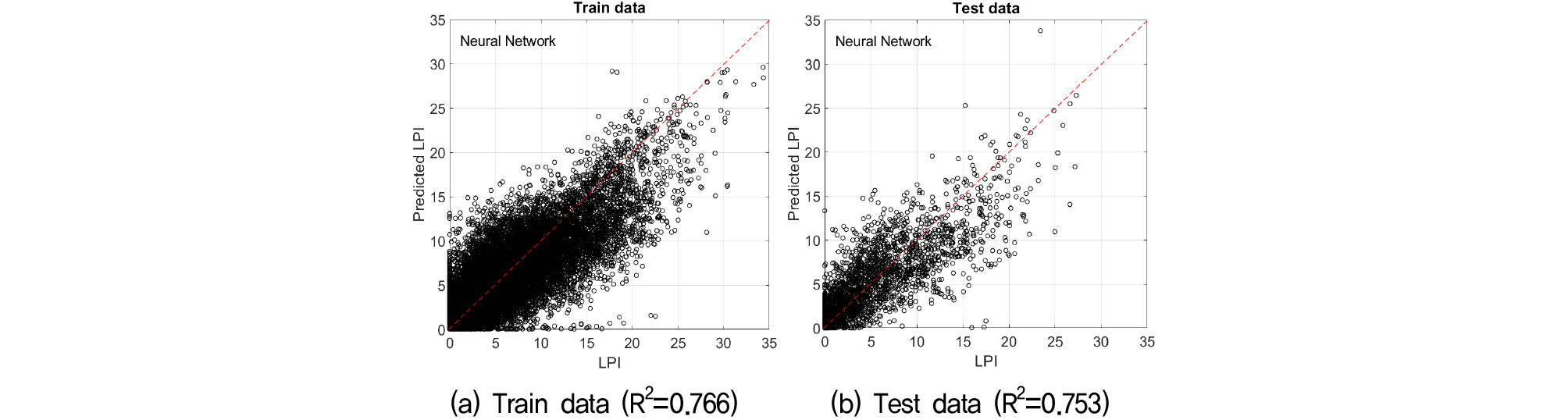
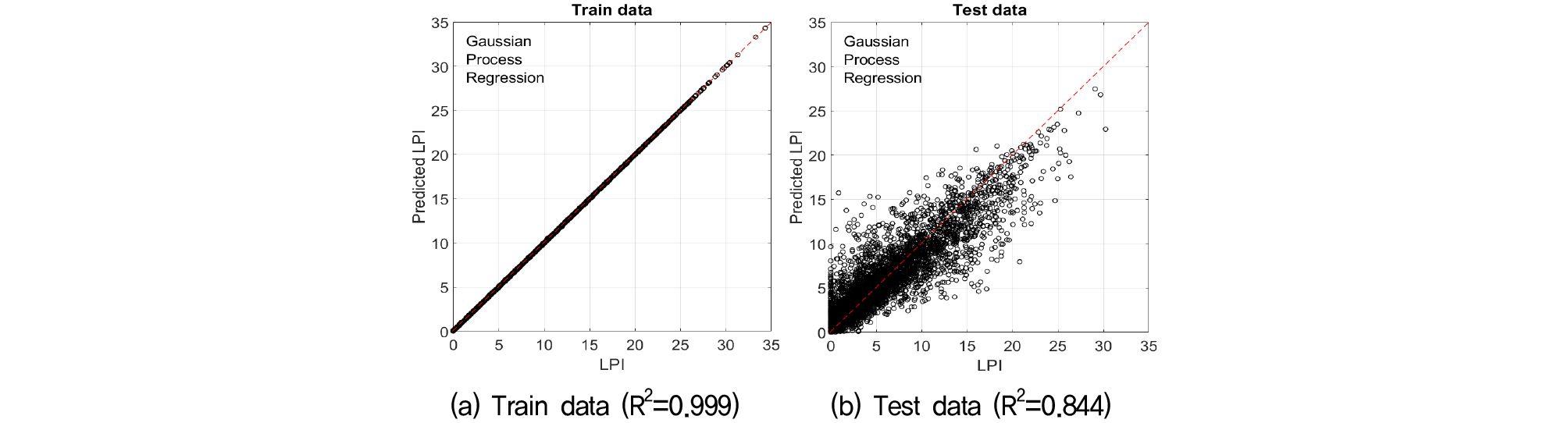
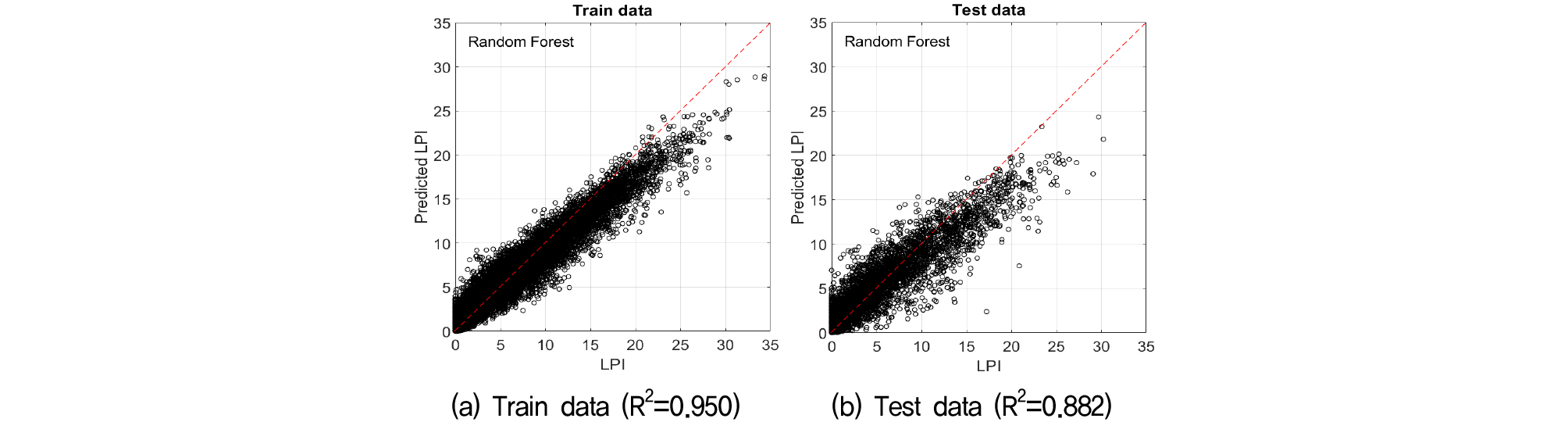
초매개변수 최적화를 통해 각 모델별 액상화 발생가능 지수의 예측 결과는 Fig. 3~5, Table 5와 같다.

https://cdn.apub.kr/journalsite/sites/jkges/2024-025-11/N0480251101/images/kges_25_11_01_F3.jpg

Fig. 3

LPI predicted from Neural Network Model

https://cdn.apub.kr/journalsite/sites/jkges/2024-025-11/N0480251101/images/kges_25_11_01_F4.jpg

Fig. 4

LPI predicted from Gaussian Process Regression Model

https://cdn.apub.kr/journalsite/sites/jkges/2024-025-11/N0480251101/images/kges_25_11_01_F5.jpg

Fig. 5

LPI predicted from Random Forest Model

Table 5.

Results for each ML

Machine Learning Model	RMSE		R²
Machine Learning Model	Train	Test	Train	Test
Neural Network (NN)	2.327	2.352	0.766	0.753
Gaussian Process Regression with exponential kernel (GPR)	0.014	1.874	0.999	0.844
Random Forest (RF)	1.077	1.629	0.950	0.882

평균제곱근오차는 학습자료 기준으로 가우시안 프로세스 회귀, 랜덤 포레스트, 인공신경망순으로 낮았으나 학습된 모델을 이용한 시험자료를 예측한 결과는 동일한 순서를 보이지 않았다. 학습된 모델을 이용한 시험자료의 결과는 랜덤 포레스트가 가장 우수했다. 반면 인공신경망은 학습과 결과 모두 가장 낮은 정밀도를 보였다.

결정계수의 경우, 학습자료 기준으로 가우시안 프로세스 회귀, 랜덤 포레스트, 인공신경망순으로 높았으며, 학습된 모델을 이용한 시험자료 예측한 결과는 랜덤 포레스트, 가우시안 프로세스 회귀, 인공신경망순으로 높았다. 가우시안 프로세스 회귀의 경우, 학습에 비해 시험자료에 대한 결정계수가 다소 낮은 값을 보였는데, 이는 새로운 자료에 대해 예측 정확도가 떨어지는 과대적합이 발생함을 의미한다. 3가지의 기계학습 모델 중 평균제곱근오차, 결정계수 및 과대적합 여부를 종합하여 랜덤 포레스트를 최종 모델로 선정하였다.

Iwasaki et al.(1978)은 액상화 지수가 5보다 작은 경우 액상화 피해가 미미하며, 15보다 큰 경우 큰 피해가 예상된다고 분류하였다. 액상화 지수 5를 기준으로 예측모델을 보면, 가로축 실제 액상화 지수 5 이상에서 1:1 점선의 아래부분은 실제 액상화 지수보다 작게 예측하는 영역이며, 윗 부분은 실제 액상화 지수보다 크게 예측하는 영역으로 볼 수 있다. 즉, 예측모델은 실제 액상화 발생가능 지수가 작은 경우 더 높은 지수값을 예상하며, 액상화 발생가능 지수가 커질수록 실제보다 낮은 액상화 발생가능 지수를 예측하는 경향을 보였다. 이는 액상화 피해위험이 큰 영역에서는 예측모델이 과소평가하고, 피해위험이 작은 영역에서는 과대평가를 함으로써 실제 사용에 있어서는 주의가 필요함을 확인하였다.

또한 실제 액상화 발생가능 지수를 계산함에 있어서 입력 지진파에 대한 지반응답해석으로 얻어진 지표면 최대가속도가 포함된다. 즉 지진파의 시간이력과 이에 따른 지반의 특성(지반감쇠 및 증폭)이 반영되나, 본 연구에서는 지진파 임의의 특징을 선택하여 학습변수로 반영함에 따라 액상화 발생가능 지수 예측의 정확도에 영향을 미친 것으로 파악된다. 보다 정확한 액상화 발생가능 지수 예측을 위해서는 지진파의 시계열 학습, 지반의 동적물성 반영 등과 같이 학습기법의 고도화 및 더 많은 특징을 고려할 필요가 있다.

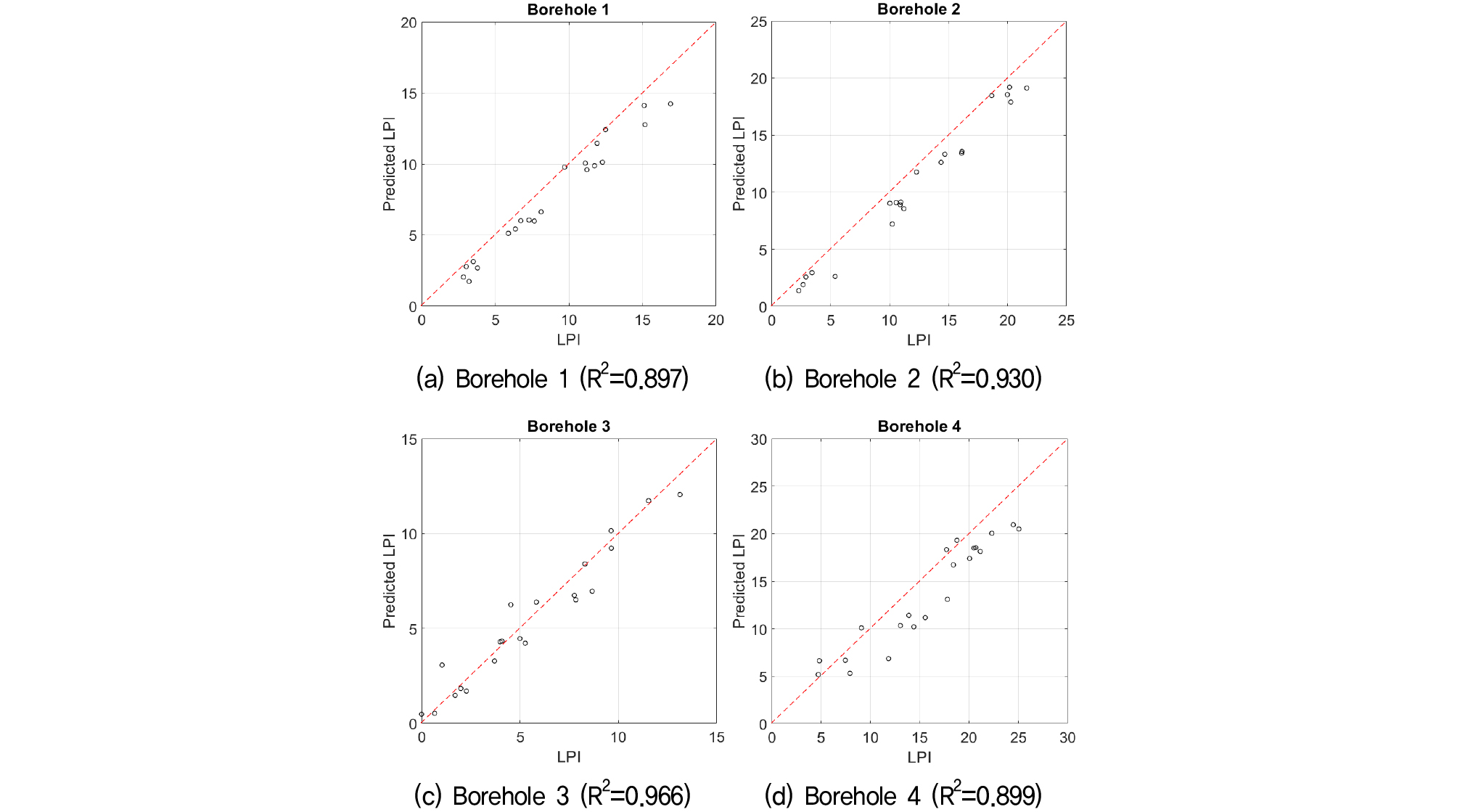
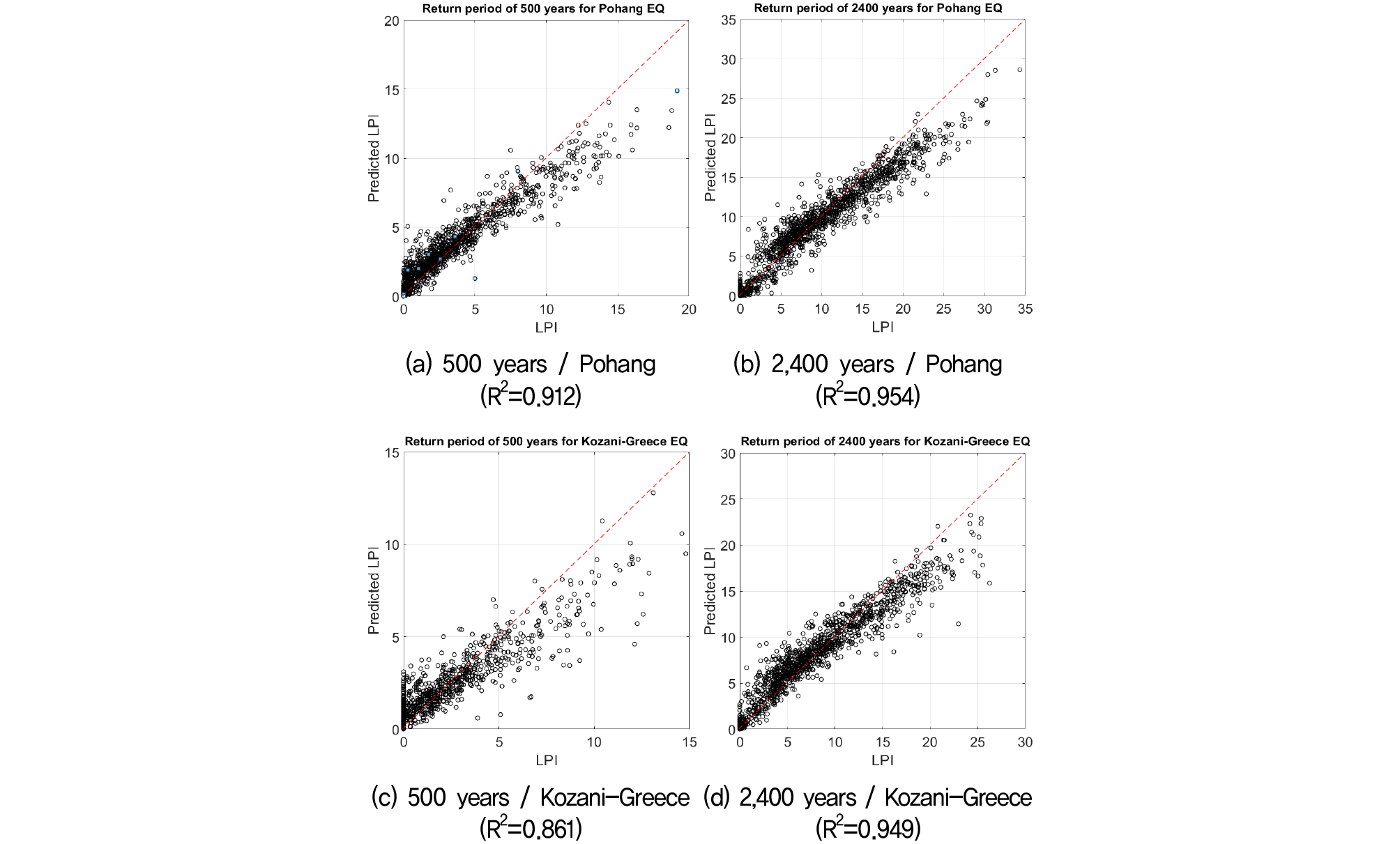
Fig. 6은 임의의 시추공 4곳을 대상으로 21개의 지진파에 대한 액상화 발생가능 지수를 예측한 결과를, Fig. 7은 재현주기 500년, 2,400년 포항, 그리스 지진파를 대상으로 액상화 발생가능 지수 예측 결과를 보여준다.

https://cdn.apub.kr/journalsite/sites/jkges/2024-025-11/N0480251101/images/kges_25_11_01_F6.jpg

Fig. 6

Predicted LPI at certain borehole

https://cdn.apub.kr/journalsite/sites/jkges/2024-025-11/N0480251101/images/kges_25_11_01_F7.jpg

Fig. 7

Predicted LPI under Pohang and Kozani-Greece Earthquake

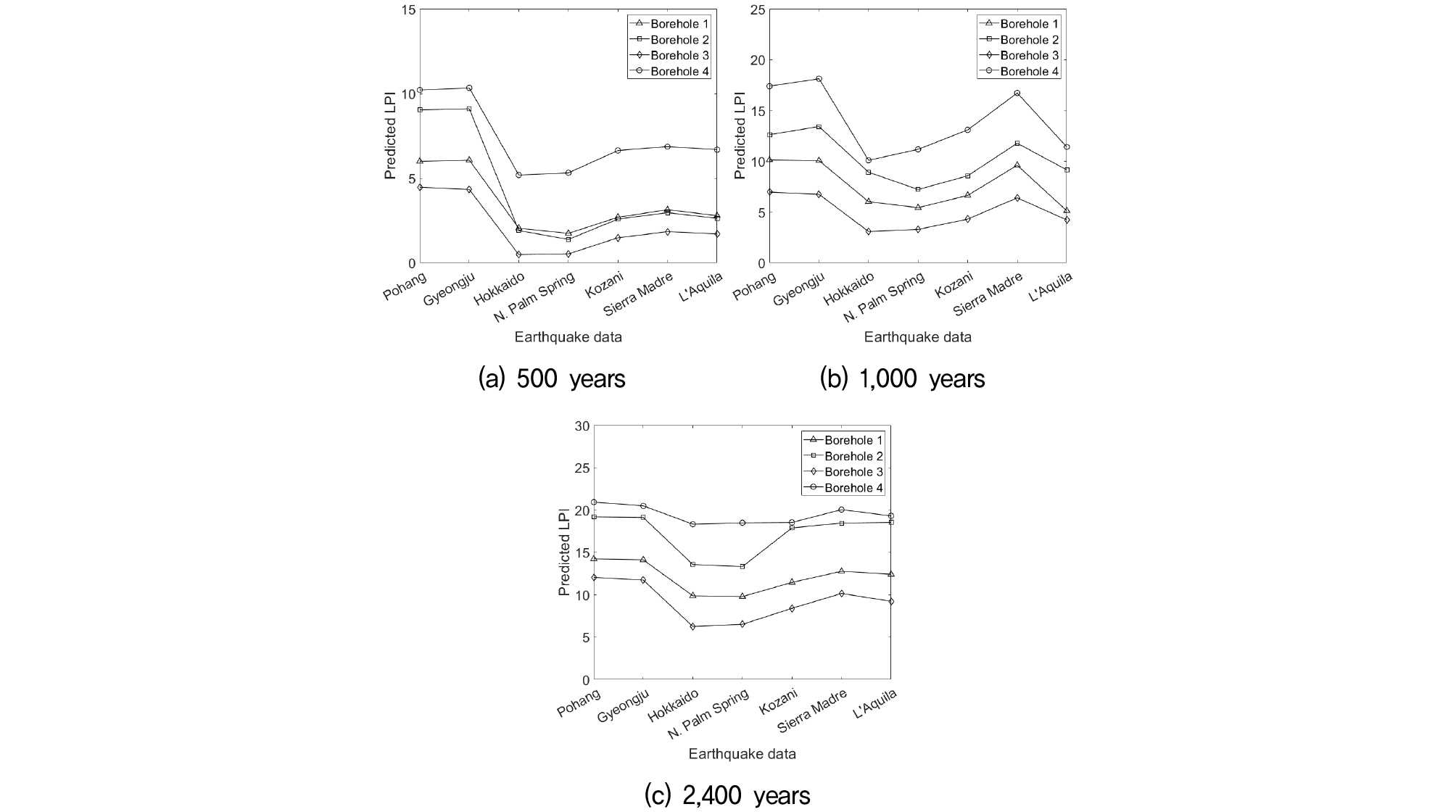
Fig. 6에서 결정계수는 최소 0.90에서 최대 0.97로 평균 0.92를 보였으며, Fig. 7에서는 최소 0.86에서 최대 0.95로 평균 0.92를 보였다. Fig. 8은 21개의 지진파(7개의 지진파, 3개의 재현주기)에 대한 예측된 액상화 발생가능 지수를 나타내었다. 시추공별 지반특성에 따라 액상화 발생가능 지수는 상이하나 지진파 변화에 따른 액상화 발생가능 지수 변화양상은 유사하게 나타났다. 이는 예측 모델이 지진파의 특성을 시추공 전체에 편향없이 반영하는 것으로 판단된다.

https://cdn.apub.kr/journalsite/sites/jkges/2024-025-11/N0480251101/images/kges_25_11_01_F8.jpg

Fig. 8

Trend in LPI under various earthquake data

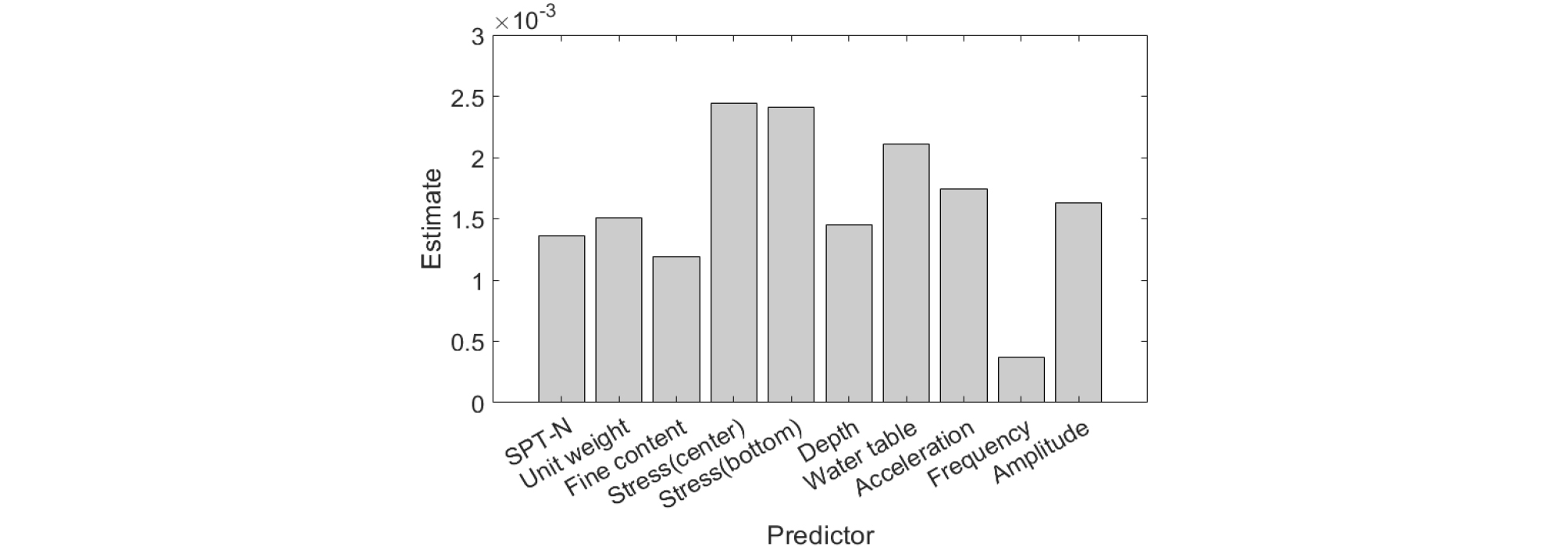
Fig. 9는 각각의 입력인자들이 랜덤 포레스트 예측모델의 학습과정에 미치는 영향을 나타낸다. 층별 중심에서의 유효연직응력(Stress(center)), 층 경계에서의 유효연직응력(Stress(bottom)), 지하수위(Water table), 최대가속도와 최소가속도의 차(Acceleration) 순으로 중요도가 나타났다. 기계학습에 있어서 특징 자료만을 입력하여 학습하므로 액상화 발생가능 지수를 계산하는 메커니즘이 고려되지 않으나, 결론적으로 학습된 결과는 실제 반복전단응력비(CSR), 반복저항응력비(CRR)에 영향을 미치는 유효연직응력, 지진특성이 반영된 것으로 확인할 수 있다.

https://cdn.apub.kr/journalsite/sites/jkges/2024-025-11/N0480251101/images/kges_25_11_01_F9.jpg

Fig. 9

Importance predictors for Random Forest model

4. 결 론

본 연구에서는 실제 시추공 자료와 지진파를 바탕으로 계산된 액상화 발생가능 지수를 이용하여 기계학습을 통해 액상화 발생가능 지수 예측을 수행하였다.

(1) 일반적인 기계학습 기법을 이용하여 사전학습을 한 결과, 앙상블, 가우시안 프로세스 회귀, 인공신경망이 낮은 평균제곱근오차(RMSE)를 보여 후보 모델로 이용하였다. 학습결과, 가우시안 프로세스 회귀, 앙상블, 인공신경망 순으로 낮은 평균제곱근오차(RMSE)를 보였으나, 시험자료를 통해 예측한 결과, 가우시안 프로세스 회귀는 과대적합된 결과를 보였다. 이에 학습 및 시험 결과를 종합하여 랜덤 포레스트 모델을 최종 모델로 선정하였다.

(2) 액상화 발생가능 지수 예측모델은 임의의 시추공, 지진파에 대해 평균 0.92의 결정계수를 보였으며, 21개의 지진파(7개의 지진파, 3개의 재현주기)의 특성을 반영하는 것으로 확인하였다. 다만, 액상화 발생가능 지수 5 이상 영역에서는 액상화 발생가능 지수를 과소예측하는 경향을 보였다.

(3) 랜덤 포레스트를 이용한 액상화 발생가능 지수 학습에 있어서 유효연직응력, 지하수위, 지진파의 최대가속도와 최소가속도의 차 순으로 중요도를 나타내었다. 단, 이는 실제 액상화 발생가능 지수에서의 인자별 중요도를 의미하지는 않는다.

(4) 본 연구에서는 7개의 대표 파형을 기초로 학습된 결과만을 사용한 한계가 있다. 따라서 추후 보다 다양한 특성을 가진 지진파 자료를 바탕으로 한 추가연구가 필요하다.

Acknowledgements

본 연구는 과학기술정보통신부 한국건설기술연구원 연구운영비지원(주요사업)사업으로 수행되었습니다(과제번호 20240104-001, AI기반 지진 시 지반 액상화 평가를 위한 데이터베이스 구축, 과제번호 20240133-001, 지반분야 재난재해 대응과 미래 건설산업 신성장을 위한 지반 기술 연구).

References

Baek, W. and Choi, J. (2019), Correlations of earthquake accelerations and LPIs for liquefaction risk mapping in Seoul & Gyeonggi-do area based on artificial scenarios, Journal of the Korean Geo-Environmental Society, Vol. 20, No. 5, pp. 5~12 (In Korean).

Baziar, M. H., Jafarian, Y., Shahnazari, H., Movahed, V. and Tutunchian, M. A. (2011), Prediction of strain energy-based liquefaction resistance of sand-slit mixtures: An evolutionary approach, Computers & Geosciences, Vol. 37, No. 11. pp. 1883~1893.

10.1016/j.cageo.2011.04.008

Chern, S. G., Lee, C. Y. and Wang, C. C. (2008), CPT-based liquefaction assessment by using fuzzy-neural network, Journal of Marine Science and Technology, Vol. 16, No. 2. pp. 139~148.

10.51400/2709-6998.2024

Fattah, E. A., Ali, H. E. A. and Ebid, A. M. (2002), Prediction of soil liquefaction using genetic programming, Proceedings of III Middle East Regional Conference on Civil Engineering Technology and III International Symposium on Environmental Hydrology, ASCE-EGS, Cairo, Egypt.

10.2139/ssrn.2761282

Goh, A. T. C. (1994), Seismic liquefaction potential assessed by neural networks, Journal of Geotechnical Engineering, Vol. 120, No. 9, pp. 1467~1480.

10.1061/(ASCE)0733-9410(1994)120:9(1467)

Goh, A. T. C. and Goh, S. H. (2007), Support vector machines: Their use in geotechnical engineering as illustrated using seismic liquefaction data, Computers and Geotechnics, Vol. 34, No. 5, pp. 410~421.

10.1016/j.compgeo.2007.06.001

Ghani, S., Sapkota, S. C., Singh, R. K., Bardhan, A. and Asteris, P. G. (2024), Modelling and validation of liquefaction potential index of fine-grained soils using ensemble learning paradigms, Soil Dynamics and Earthquake Engineering, Vol. 177, pp. 108399.

10.1016/j.soildyn.2023.108399

Iwasaki, T., Tatsuoka, F., Tokida, K. -I., and Yasuda, S. (1978), A practical method for assessing soil liquefaction potential based on case studies at various sites in Japan, Proceedings of the 2nd International Conference on Microzonation for Safer Construction Research and Application, NSF, San Francisco, USA, pp. 885~896.

Jas, K. and Dodagoudar, G. R. (2023), Explainable machine learning model for liquefaction potential assessment of soils using XGBoost-SHAP, Soil Dynamics and Earthquake Engineering, Vol. 165, pp. 107662.

10.1016/j.soildyn.2022.107662

Juang, C. H., Yuan, H., Lee., D.H. and Lin., P.S. (2003), Simplified cone penetration test-based method for evaluating liquefaction resistance of soils, Journal of Geotechnical and Geoenvironmental Engineering, Vol. 129, No. 1. pp. 66~80.

10.1061/(ASCE)1090-0241(2003)129:1(66)

Kohestani, V. R., Hassanlourad, M. and Ardakani, A. (2015), Evaluation of liquefaction potential based on CPT data using random forest, Natural Hazards, Vol. 79, pp. 1079~1089.

10.1007/s11069-015-1893-5

Ozsagir, M., Erden, C., Bol, E., Sert, S. and Özocak, A. (2022), Machine learning approaches for prediction of fine-grained soils liquefaction, Computers and Geotechnics, Vol. 152, pp. 105014.

10.1016/j.compgeo.2022.105014

Pal, M. (2006), Support vector machines-based modelling of seismic liquefaction potential, International Journal for Numerical and Analytical Methods in Geomechanics, Vol. 30, No. 10, pp. 983~996.

10.1002/nag.509

Sabbar, A. S., Chegenizadeh, A. and Nikraz, H. (2019), Prediction of liquefaction susceptibility of clean sandy soils using artificial intelligence techniques, Indian Geotechnical Journal, Vol. 49. pp. 58~69.

10.1007/s40098-017-0288-9

Samui, P. and Sitharam, T. G. (2011), Machine learning modelling for predicting soil liquefaction susceptibility, Natural Hazards and Earth System Sciences, Vol. 11, pp. 1~9.

10.5194/nhess-11-1-2011

Journal of the Korean Geo-Environmental Society ISSN:1598-0820(Print) 2714-1233(Online) 한국지반환경공학회 논문집

Preview

Study of Prediction of Liquefaction Potential Index Based on Machine Learning Method

ABSTRACT

MAIN

(1)

Fig. 1

Horizontal acceleration seismic waves matched with a return period of 2,400 years

Table 1.

Earthquake information considered in this study

Fig. 2

Considered features obtained from the earthquake record

Table 2.

Considered features for LPI prediction

Table 3.

Results of selecting appropriate ML model for LPI prediction

Table 4.

Results of hyperparameter optimization

Fig. 3

LPI predicted from Neural Network Model

Fig. 4

LPI predicted from Gaussian Process Regression Model

Fig. 5

LPI predicted from Random Forest Model

Table 5.

Results for each ML

Fig. 6

Predicted LPI at certain borehole

Fig. 7

Predicted LPI under Pohang and Kozani-Greece Earthquake

Fig. 8

Trend in LPI under various earthquake data

Fig. 9

Importance predictors for Random Forest model

Acknowledgements

References