1. Introduction

The propagation of elastic waves in soil is a critical research area in geological engineering, earthquake engineering, and civil engineering. These waves, generated by earthquakes, explosions, mechanical vibrations, and other sources, are significantly influenced by the physical and mechanical properties of the soil medium during their transmission. Understanding this wave phenomenon is essential for predicting and mitigating earthquake disasters, optimizing civil engineering designs, and improving subsurface resource exploration. While much research has focused on wave propagation in homogeneous soils, the complex nature of heterogeneous soils presents additional challenges that require further exploration.

Numerous scholars, both domestically and internationally, have studied the propagation characteristics of elastic waves in various contexts (Hall Jr & Richart Jr, 1963; Hardin & Richart Jr, 1963). For instance, Larson and colleagues optimized mine detection systems by investigating wave propagation in soil, assessing propagation characteristics and identifying nonlinear mechanisms (Larson et al., 2002). Wang et al. analyzed the effects of the number of joints on stress wave propagation and stress wave conversion in rock masses (Wang et al., 2023). Cai et al. (2009) examined the displacement generated by a row of elastic piles in a homogeneous, unbounded, porous elastic soil after the passage of an elastic wave. Li et al. (2023) derived a simplified analytical solution for the seismic response of a tunnel cross-section in horizontally layered strata under oblique incidence of SH waves. These studies, while providing valuable insights, are primarily centered on homogeneous soils, and more nuanced understanding is needed regarding the effects of soil heterogeneity on wave propagation.

In recent years, the impact of soil moisture content on wave propagation has also gained attention. Studies on both saturated and unsaturated soils reveal significant differences in wave behavior. Shin et al. (2016) examined the theoretical aspects of elastic wave velocity in unsaturated soils. Yi et al. (2019) investigated the transient wave propagation characteristics in a mixed-phase ground with an ideal interface between a dry layer and a saturated layer. Kumar et al. (2021) analyzed the reflection and refraction of plane waves at the interface between elastic solids and partially saturated soils. However, the combined effects of heterogeneity and moisture content on wave propagation still require more detailed investigation. Building on this foundation, this paper analyzes the variation of wave velocity with soil saturation and the attenuation associated with degree of saturation.

In geological engineering and civil engineering design, the mechanical properties of soils are usually assumed to be homogeneous and continuous. However, natural geomaterials such as soils and rocks possess inherent heterogeneity. This heterogeneity stems from complex geological processes, including deposition, weathering, and fracturing, leading to significant spatial variability in material properties, profoundly impacting the stability and safety of engineering structures. Therefore, a deeper understanding of the propagation characteristics of waves in heterogeneous soils is crucial for ensuring structural safety and improving design reliability.

Several studies have attempted to address the challenges of wave propagation in heterogeneous soils. For example, Manolis et al. (1999) introduced methods for analyzing elastic waves propagating in two-dimensional elastic heterogeneous media, while Chammas et al. (2003) used the finite element method to assess whether Rayleigh waves in heterogeneous soil can be used to estimate average elastic parameters. He (2010) introduced five physical tools for imaging and interpreting the heterogeneity of geophysical properties. Wang and Sett (2016) used finite element simulations to model the time-domain response of uncertain seismic waves propagating through uncertain heterogeneous solids. El Haber E et al. (2019) evaluated the impact of two-dimensional spatial variability on surface ground motion through numerical experiments. Their results indicate that heterogeneity significantly affects the wavenumber and dissipation of shear waves. These studies highlight the complexity of wave propagation in Heterogeneous media and show that the propagation characteristics of waves in Heterogeneous media need further analysis and improvement.

This paper explores the propagation of elastic waves in heterogeneous soils, focusing on spatial variability and moisture content. Most studies use the finite element method (FEM), but the finite difference method (FDM) was chosen in this study because it offers higher efficiency in handling dynamic wave propagation problems. With its explicit time-stepping approach, FDM is better suited for capturing the subtle changes in wave propagation. Additionally, FDM is easier to implement with regular grids, simplifying numerical calculations, and it provides better numerical stability when dealing with heterogeneous media with spatial variability. Therefore, this study uses FLAC 2D 8.0 (Itasca Consulting Group, Inc., 2016) finite difference software to simulate wave propagation under different variability parameters. A random field model, combined with the Monte Carlo method, generates soil parameter data to reflect realistic variability, enhancing design reliability. The study analyzes the effects of correlation lengths, variability, and saturation on wave velocity, amplitude attenuation, and waveform changes, providing valuable insights for improving structural safety and design effectiveness.

2. Spatial variability

Soil properties exhibit uncertainty, which can generally be attributed to measurement errors, model uncertainties, and system-related errors. The uncertainty in soil properties can be categorized into aleatory uncertainty and epistemic uncertainty (Lacasse & Nadim, 1997). Stochastic uncertainty represents the inherent randomness of properties, thus it is a function of the spatial variability of those properties.

Soil spatial variability is an important concept describing how soil properties change spatially. Soil properties are not uniformly distributed but exhibit natural heterogeneity due to complex geological processes such as soil formation and environmental conditions. The spatial variability characteristics of soil can be described using central tendency (or mean value), coefficient of variation, correlation length, and anisotropy. Due to the complex spatial variability of soil, analysis and modeling of the variability of properties can be simplified.

3. Simulation

3.1 Random Field

To simulate the spatial variability of soil properties, random field models are commonly used. The simulation of random fields helps to quantify uncertainty probabilistically and can be used to describe the random variation characteristics of soil properties in space. Common random field models include Gaussian random fields and non-Gaussian random fields (e.g., Markov random fields).

The assumption of Gaussian behavior can greatly simplify random problems. Most simulation methods produce fields that either approximately follow a Gaussian distribution or fully comply with Gaussian analysis. Gaussian fields only require specifying the mean and covariance function for each pair of points. In contrast, for general non-Gaussian fields, a complete specification requires providing all n-dimensional joint distribution functions for any n points in the field, which is usually impractical. In this study, a Gaussian random field model is used to simulate the spatial variability of soil properties. The advantage of the Gaussian random field model lies in its mathematical simplicity and well-established theoretical analysis. Using a Gaussian random field model, soil property distributions with given means and variances can be generated, thereby simulating the spatial variability of actual soil.

3.2 Monte Carlo Method

The Monte Carlo Method (MCM) is a computational technique for numerical simulation by generating appropriate random numbers. It is particularly suitable for dealing with problems involving uncertainty and multiple variables. By repeatedly generating random samples, the probability distribution of the results can be obtained.

Generally, conducting a probabilistic analysis using the Monte Carlo Method requires multiple trials. As the number of trials increases, the confidence level of the resulting data increases. The required number of Monte Carlo trials depends on the desired confidence level of the solution and the number of variables considered (Harr, 1987). This can be estimated as follows.

Here, N_mc is the number of Monte Carlo trials, d is the standard normal deviation corresponding to the confidence level, ε is the desired confidence level expressed in decimal form (0 to 100%), and m is the number of variables. The number of Monte Carlo trials increases geometrically with the confidence level and the number of variables. Assuming a confidence level of 90%, a standard normal deviation of 1.64, and one variable, the number of Monte Carlo trials is approximately 67.

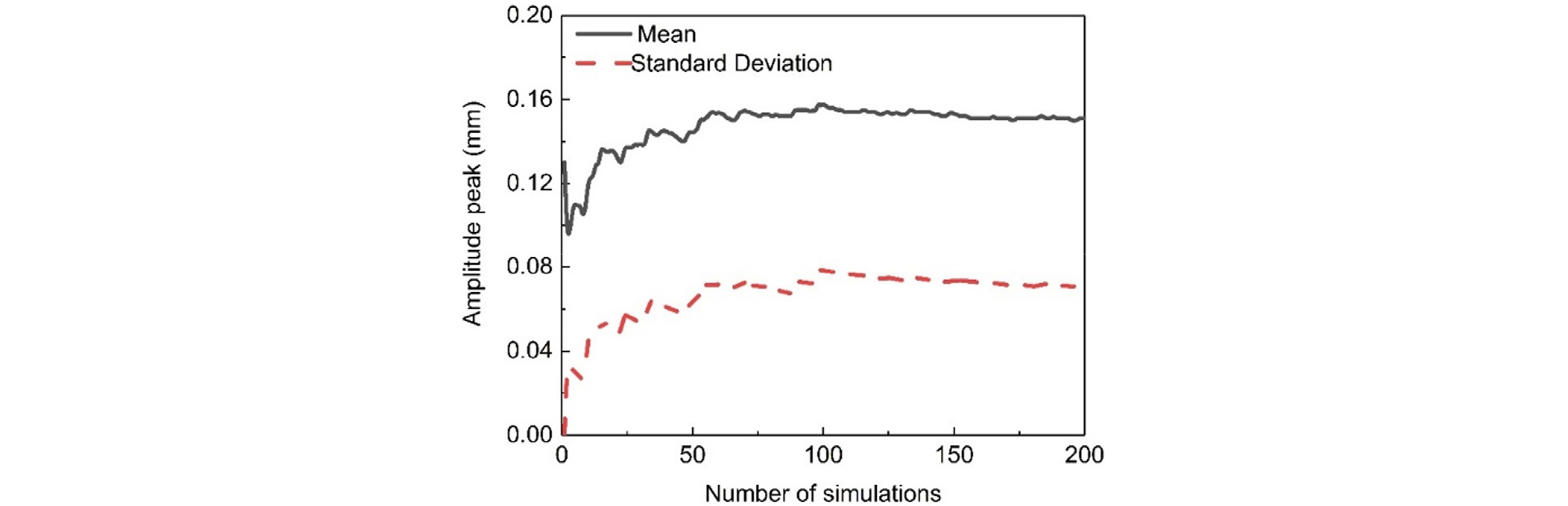
To reduce computational effort and obtain reliable simulation results of random fields, this paper uses clay as an example (density of 1,700 kg/m³, elastic modulus of 2.0E+8 Pa, Poisson’s ratio of 0.33, and porosity of 0.638). By taking the elastic modulus as the variable parameter, a random model is analyzed (with a coefficient of variation (COV) of 30% and a correlation length of 0.05 m). Fig. 1 shows the relationship between the mean and standard deviation of the peak amplitude of compressional wave velocity and the number of simulations. As seen in the Fig. 1, the mean and standard deviation of the peak amplitude become stable at around 150 simulations. However, the numerical simulation results are more accurate with 200 simulations; hence, this paper uses 200 simulations.

Fig. 1

Convergence of the mean and standard deviation of the compressional wave velocity amplitude peak with the number of simulations (COV=30%, ζ=0.05m）

3.3 Generation of Heterogeneous Ground

In this study, the generation of soil heterogeneity uses the ‘RandomFields’ package in R to generate Gaussian random fields (Schlather, 2001). The values of this random field follow a normal distribution, which can include negative values. Since soil parameters (e.g., elastic modulus) cannot be negative, applying a logarithmic transformation to avoid negative values. By transforming the natural logarithm values of the generated Gaussian random field back to the original scale, we obtain a lognormal random field. The lognormal distribution ensures that all values are positive, which aligns with the physical properties of actual soil parameters.

The random fields generated in R can control the characteristics of variability by explicitly setting relevant parameters (such as the coefficient of variation and spatial correlation length), effectively simulating the heterogeneity of the soil. Additionally, this paper uses the Monte Carlo method to generate 200 sets of random field data, which are then subjected to statistical analysis. The mean, variance, and other statistical indicators are calculated from these 200 sets of data to evaluate the reliability and uncertainty of the model predictions.

4. Wave Propagation in Heterogeneous Soil

In this study, the establishment and analysis of the two-dimensional model aim to explore the propagation characteristics of elastic waves in heterogeneous soils. Clay is again used as an example for numerical simulation in this section.

4.1 Effects of Spatial Variability Parameters

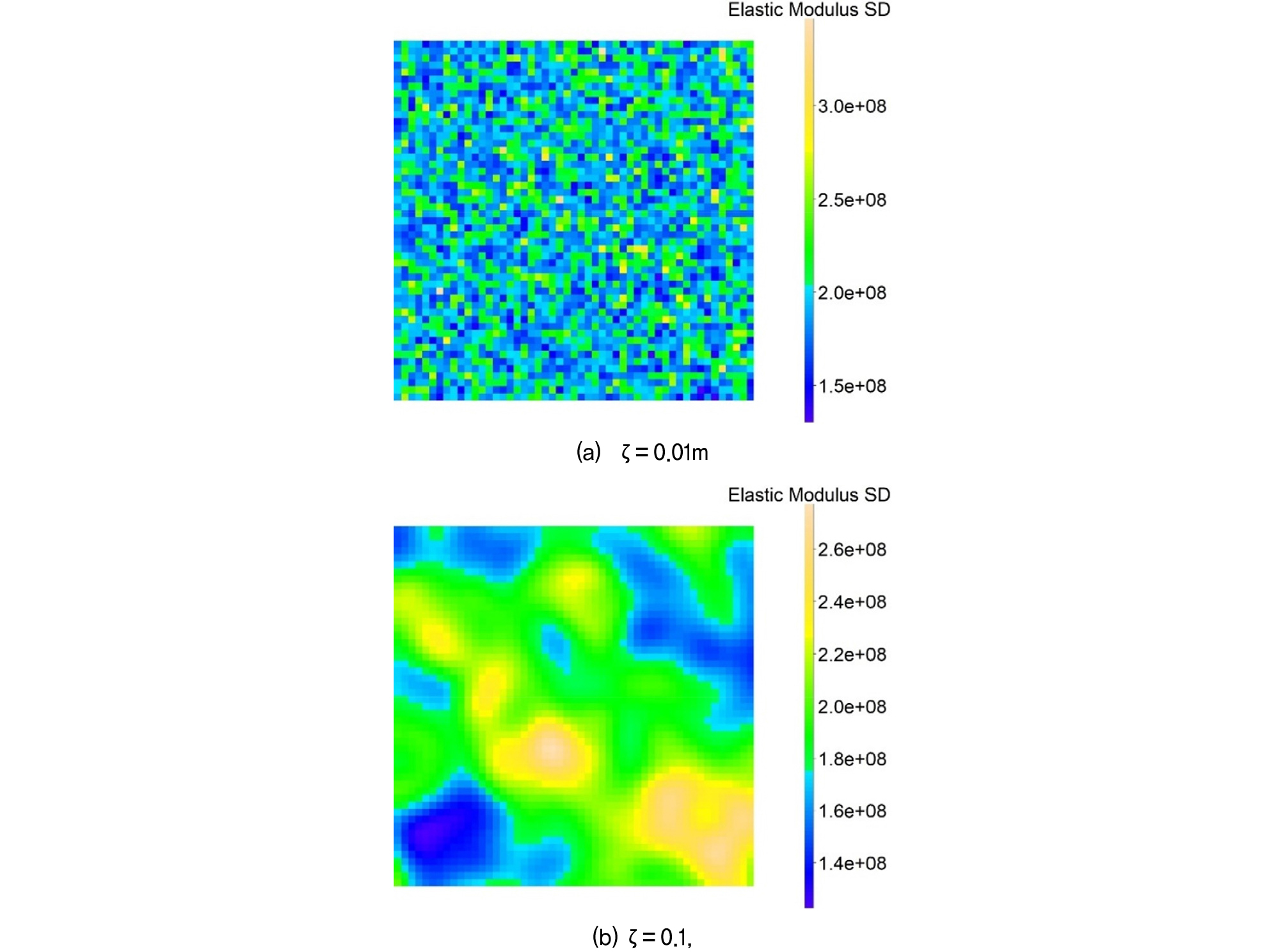
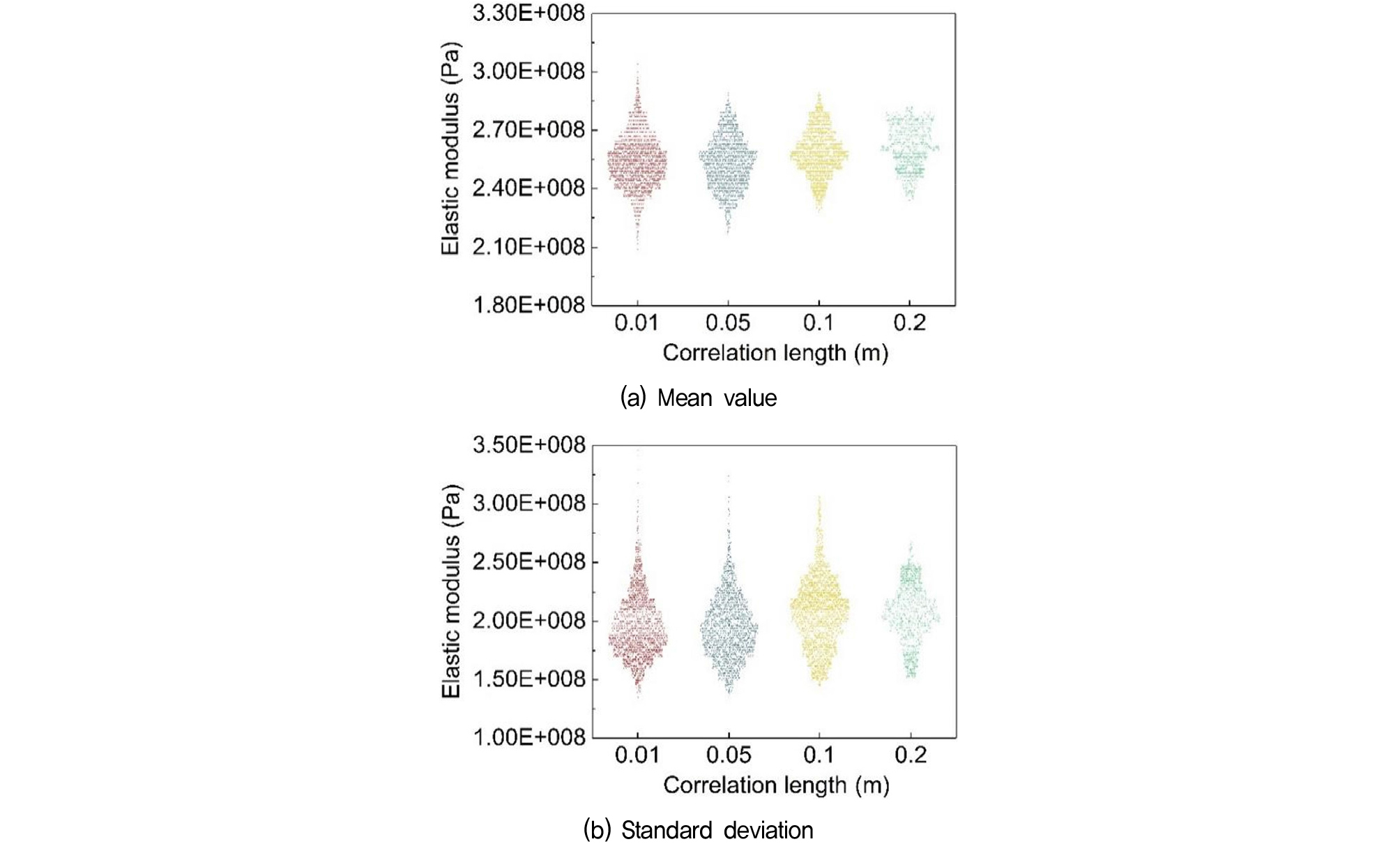
When simulating the propagation characteristics of elastic waves in heterogeneous soils, parameters affecting spatial variability (such as the coefficient of variation and correlation length) have a significant impact on wave propagation. This section uses a rectangular model with a side length of 0.5 m, where each side is divided into 50 equal grids. The coefficient of variation of the elastic modulus is assumed to be 30%, and the Monte Carlo simulation is set to 200 trials. Using the elastic modulus as the variable parameter, random fields with correlation lengths of 0.01, and 0.1 meters can be obtained. Since the standard deviation (SD) better represents the dispersion degree of the random field, the generated random field data’s standard deviation (Fig. 2) and the distribution of elastic modulus data obtained from 200 trials (Fig. 3) are presented as examples.

Fig. 2

Variation of elastic modulus random field characteristics with correlation length ζ

Fig. 3

Distribution of elastic modulus at different correlation lengths

From Figs. 2-3, it can be observed that with smaller correlation lengths, the values of the random field change more dramatically within a smaller range, showing strong fluctuations. The values at adjacent points have weak correlations, indicating high variability at a small scale. With larger correlation lengths, the values of the random field change more gradually over a larger range, exhibiting a strong smoothing effect. The values at adjacent points are highly correlated, meaning the random field shows consistency over a large scale. Additionally, the distribution of the random field data for elastic modulus resembles a normal distribution. This is because the random field data was generated using a Gaussian random field model, which assumes the data follows a normal distribution. The log transformation ensures that all values are positive, making the data more realistic for soil parameters. As the correlation length increases, the range of fluctuations in the mean and standard deviation decreases. Short correlation lengths lead to significant local fluctuations, while long correlation lengths result in more uniformly distributed values, creating a smoother distribution that aligns with the characteristics of a normal distribution. Furthermore, by generating 200 sets of random data using the Monte Carlo method, extensive simulation and statistical analysis lead to stable means and variances, further reinforcing the normal distribution characteristics of the data.

4.2 Wave Propagation

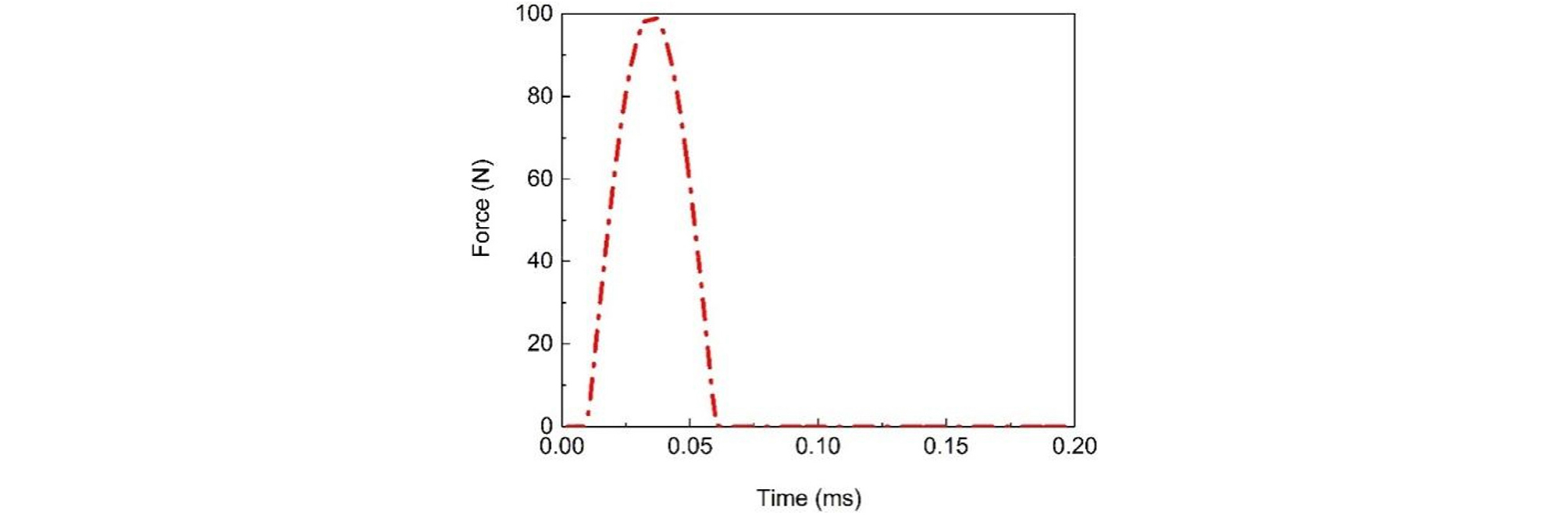
The random fields generated in R are applied to the finite difference grid. The model created using the finite difference method matches the model generated in R. The model is a square ground with a side length of 0.5 meters, divided into 50 grids per side, resulting in a total of 2,500 finite difference grids (Fig. 4). The left, right, and bottom boundaries are set as quiet boundaries in the x and y directions, and the top boundary is a free boundary. A half-period sine wave excitation is applied at the midpoint of the top boundary (Load), as shown in Fig. 5. Points M1 to M5 are monitoring points.

Fig. 4

Case model

Fig. 5

Excitation load

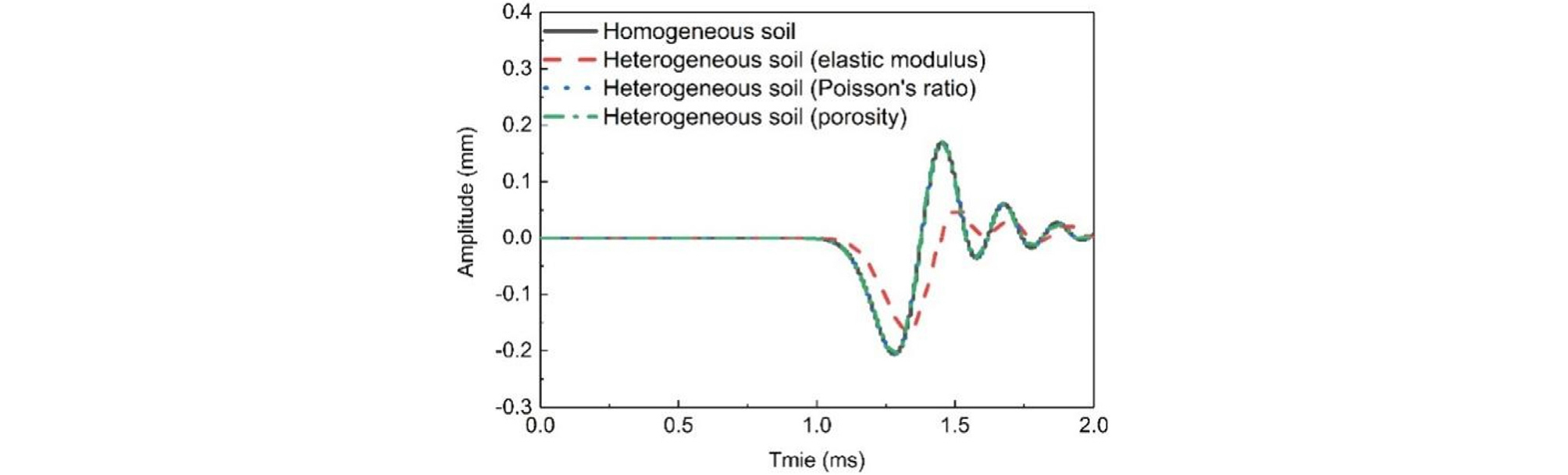
Fig. 6 shows the compressional wave responses of homogeneous and heterogeneous clay under the excitation of a half-period sine wave. It is evident that the response of compressional waves in heterogeneous clay is delayed compared to that in homogeneous clay. In heterogeneous clay, the physical properties (such as Poisson’s ratio, elastic modulus, and porosity) vary at different locations, resulting in varying wave speeds. As the wave travels through the heterogeneous medium, its speed changes continuously, leading to a more complex propagation path and increased travel time. Additionally, due to the variations in physical properties, heterogeneous ground may exhibit different levels of absorption and attenuation, which reduces the wave’s energy and propagation speed, further delaying the response time.

Fig. 6

Fluctuation response of compression waves on homogeneous ground and heterogeneous ground

From Fig. 6, it can be observed that for the cases where Poisson’s ratio and porosity are the variable parameters, the wave responses are almost identical to those in homogeneous soil. The significant differences arise due to variations in the elastic modulus, indicating that the spatial variability of the elastic modulus in heterogeneous soil has a substantial impact on wave propagation.

The findings from this study regarding the delay in the propagation of compressional waves in heterogeneous soils are consistent with those reported by Song (2013). In song’s work, the influence of ground heterogeneity on wave propagation was highlighted through stochastic numerical analysis, indicating that the variability in material properties such as elastic modulus and correlation length significantly affects the wavefront and travel-time delays. Similarly, the present study demonstrates that variations in physical properties like elastic modulus in heterogeneous soil lead to delayed wave responses and altered wave speeds, in agreement with Song’s findings. This comparison supports the validity of the results and emphasizes the critical role of spatial variability in wave propagation studies.

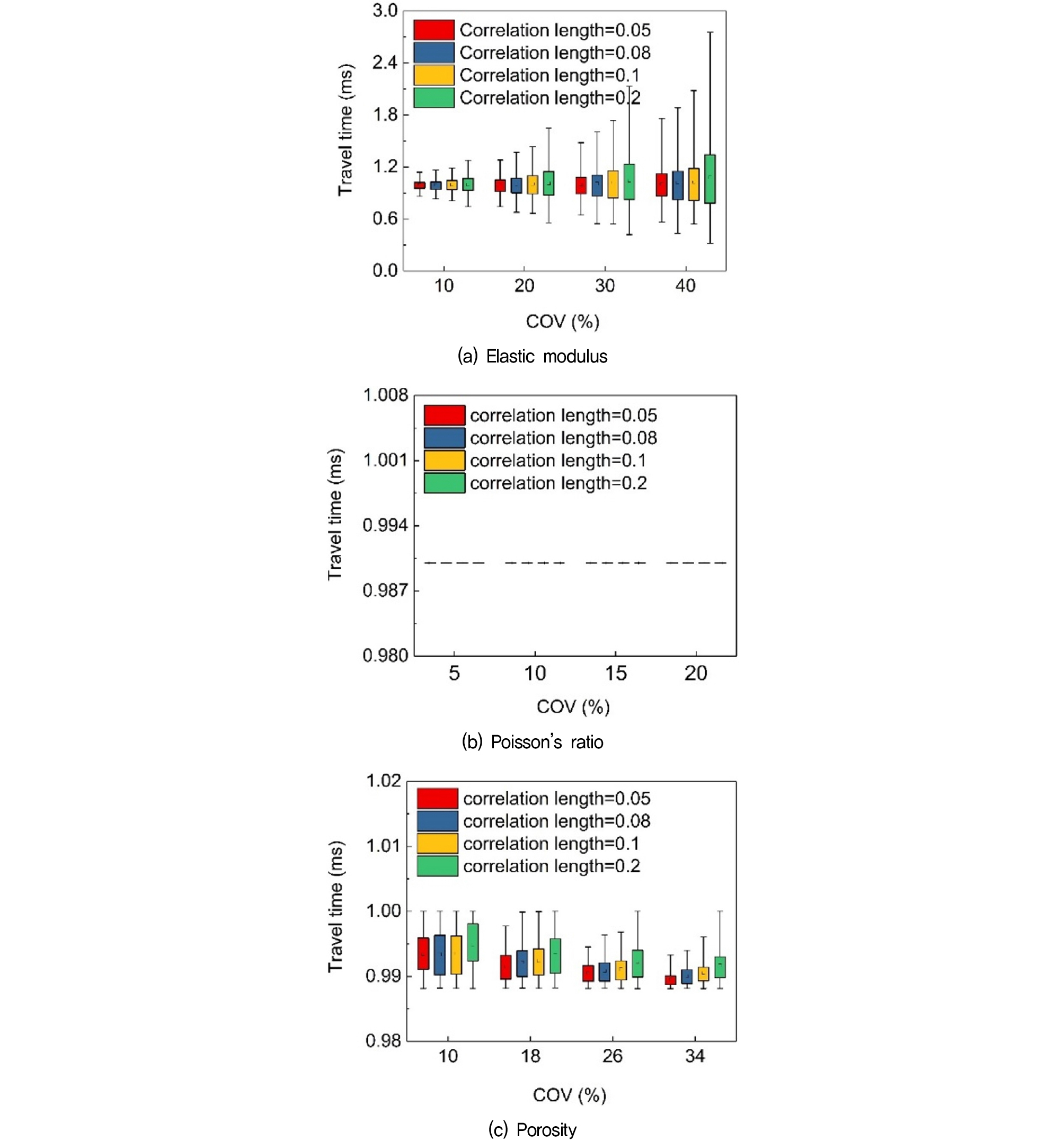
When studying the propagation characteristics of waves in heterogeneous soils, the impact of the coefficient of variation and correlation length are critical factors that cannot be ignored. These parameters not only determine the spatial variability of soil properties but also significantly influence the wave propagation path, speed, and energy transmission characteristics. This section will discuss in detail the effects of these parameters on wave propagation characteristics. Such an analysis helps to understand how the spatial variability of soil affects the propagation of elastic waves in heterogeneous soils. Using point M3 as an example, this section monitors the propagation time of waves reaching point M3 after an excitation load is applied and conducts a statistical analysis of 200 test results. The specific effects of the coefficient of variation and correlation length on wave propagation time are shown in Fig. 7.

Fig. 7

The impact of coefficient of variation and correlation length on compressional wave propagation time

Fig. 7 shows the impact of the coefficient of variation and correlation length on the propagation time of compressional waves in heterogeneous soils with different variability parameters. From Fig. 7(a), when the elastic modulus is the variability parameter, the time for the wave to reach point M3 increases as the coefficient of variation and correlation length increase. Changes in the shear modulus affect the stiffness of the material, thereby influencing the wave propagation speed. As the coefficient of variation increases, ground heterogeneity increases, which enhances the fluctuation and scattering of material properties, making the wave propagation path more complex and thus increasing the wave arrival time.

When porosity is the variability parameter (Fig. 7(c)), the mean wave propagation time of 200 trials increases with an increase in correlation length. However, as the coefficient of variation increases, the wave propagation time decreases. An increased coefficient of variation means a wider range of porosity changes. Since high porosity areas offer greater resistance, waves may travel through low porosity regions, reducing the arrival time. Moreover, a high coefficient of variation might lead to changes in local reflection and absorption characteristics, and the interaction of these effects may also reduce the arrival time. As the correlation length increases, it implies that larger areas have similar properties, smoothing out the property variations along the wave propagation path. However, since this study focuses on clay, which has high porosity, an increase in correlation length leads to large-scale discontinuities. The monitoring point being in this high porosity area results in decreased stiffness and density, thereby slowing the wave speed and increasing the wave propagation time.

Fig. 7 shows that the variability of the elastic modulus has a particularly significant impact on wave propagation time because the elastic modulus directly determines the stiffness and wave speed of the medium. A larger coefficient of variation in the elastic modulus causes greater local wave speed variations, making the wave propagation path more complex. In contrast, the variability of the Poisson’s ratio and porosity has a smaller impact on propagation time, especially for the Poisson’s ratio (Fig. 7(b)), where the propagation time remains nearly unchanged with changes in the coefficient of variation and correlation length. This indicates that these parameters play a relatively minor role in the wave propagation process.

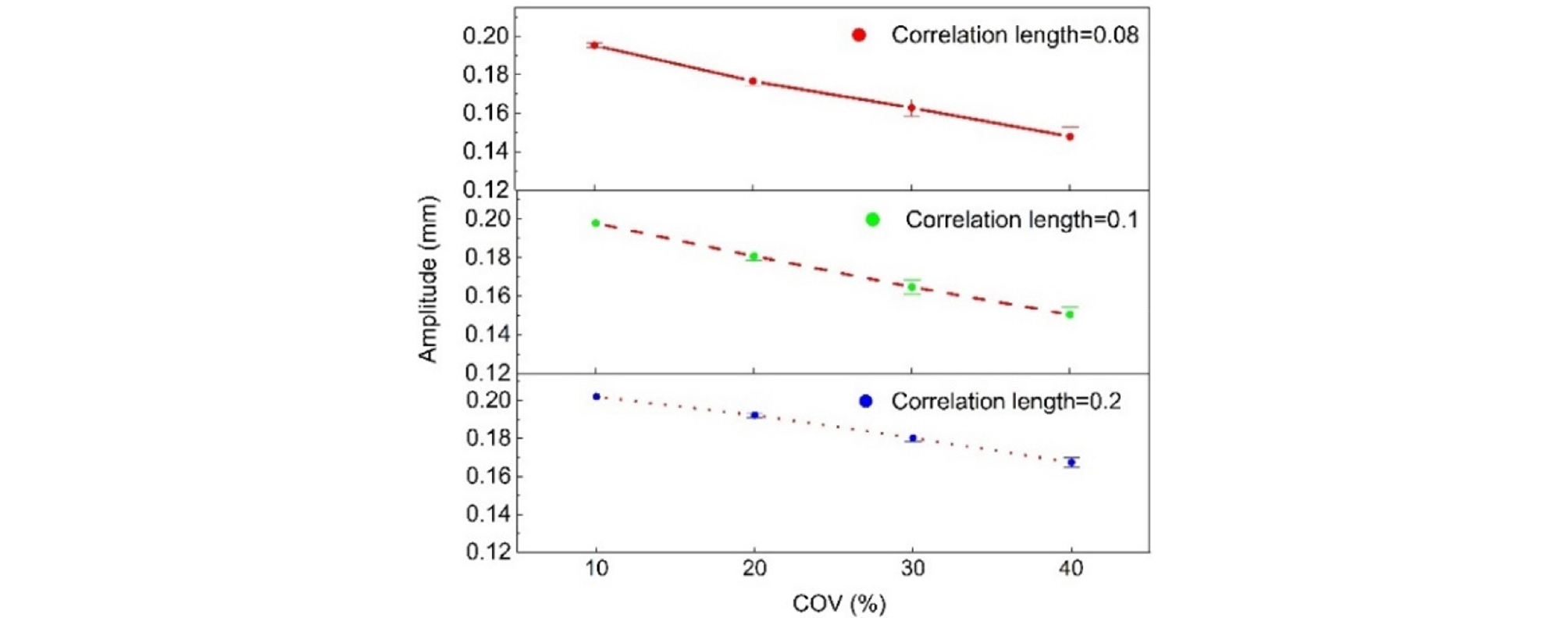
Details on the variations in the peak amplitude of compressional waves in heterogeneous soils can be found in Fig. 8. As can be seen from Fig. 6, since the variation parameters Poisson’s ratio and porosity have little impact on wave propagation, the M3 point with the elastic modulus as the variation parameter is used as an example. For 200 tests, a statistical analysis of the changes in the peak amplitude of the compression wave at point M3 under different variation coefficients and correlation lengths is conducted. The changes in peak amplitude reflect the concentration and transmission of energy as the wave propagates through the medium. By analyzing the effects of the coefficient of variation and correlation length on the peak amplitude, the efficiency of wave energy transmission under different soil conditions can be evaluated.

Fig. 8

The impact of coefficient of variation and correlation length on the peak amplitude of compressional waves

Fig. 8 shows that the peak amplitude of compressional waves decreases as the coefficient of variation increases. The variability of the elastic modulus has a significant impact on the peak amplitude. When the coefficient of variation is high and the correlation length is short, the local energy variations of the wave are pronounced, leading to significant changes in peak amplitude and a rapid decrease in the peak value.

As the coefficient of variation increases, the peak amplitude decreases. This is because the increase in the coefficient of variation enhances the heterogeneity of the soil, resulting in more frequent scattering and reflection of energy during wave propagation, which leads to energy dispersion and a reduction in amplitude. Additionally, a larger coefficient of variation complicates the wave propagation path, causing continuous energy dissipation during transmission. Comparing the changes in peak amplitude across four different correlation lengths, it is evident that the decrease in peak amplitude with increasing coefficient of variation slows down as the correlation length increases. This is because, at larger correlation lengths, soil property variations are more gradual, and the correlation between adjacent points is stronger, making the wave propagation path more continuous and smoother, thus reducing energy scattering and reflection. Consequently, although the coefficient of variation still affects wave propagation, its impact is smoothed out by the larger correlation length, leading to a more stable change in peak amplitude.

According to Figures 7 and 8, the changes in P-wave travel time and peak amplitude with increasing geological heterogeneity are consistent with the findings of Song (2013). This study indicates that increased geological heterogeneity significantly prolongs wave travel time due to the variation in material properties (such as elastic modulus and density) across different geological layers, leading to uneven wave speeds. Specifically, as waves travel through a medium with high heterogeneity, variations in wave speeds across different regions cause deformation and spreading of the wavefront, thereby increasing the travel time. Additionally, such heterogeneity can result in multipath propagation and scattering effects of energy, making the peak amplitude of the wave attenuate more significantly during propagation. The observed trend in our data shows that in regions with higher heterogeneity, wave delays are more pronounced, and the peak amplitude exhibits attenuation, which is also consistent with Song’s findings.

4.3 Wave Attenuation

The attenuation characteristics of waves reflect the degree of energy loss during wave propagation, which is crucial for engineering design related to seismic wave early warning and structural seismic performance. Changes in the coefficient of variation (COV) and correlation length lead to varying degrees of energy loss during wave propagation. By analyzing the mean and standard deviation of different variation parameters (elastic modulus, Poisson’s ratio, and porosity), the impact of COV and correlation length on wave attenuation can be better understood, shedding light on wave propagation characteristics in heterogeneous soils.

As shown in Fig. 4, based on the peak amplitude at the excitation point at the top of the model (A1) and the peak amplitude of the output wave at point M5 at the bottom of the model (A2), the attenuation of compression waves and shear waves can be calculated (Santamarina et al., 2001).

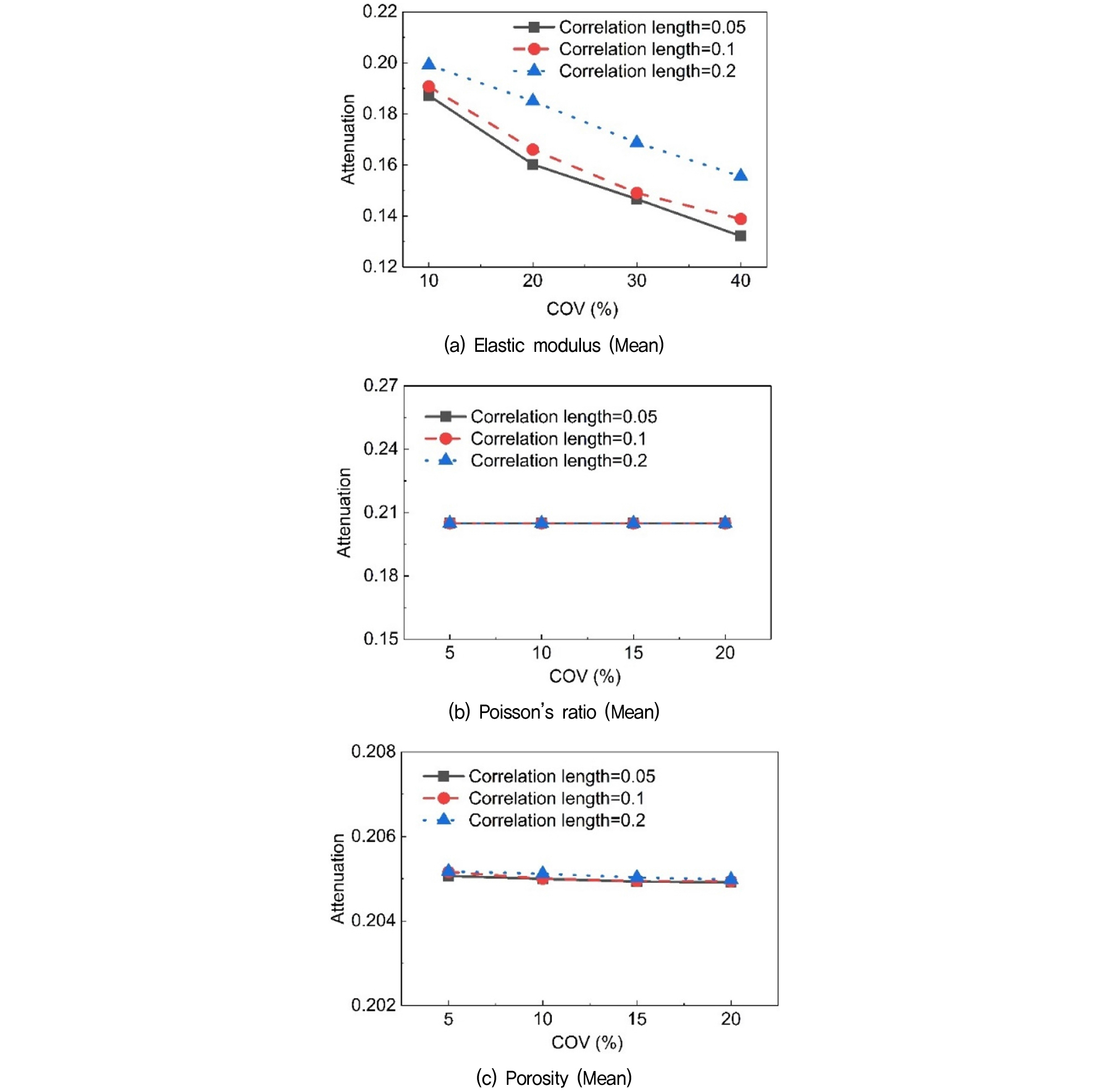
In this section, points M1 and M4 are selected to analyze the attenuation of waves during propagation. For each Monte Carlo simulation, the ratio of the peak values of the vibrational waves at the two monitoring points is calculated to obtain the attenuation for one trial. Then, a statistical analysis is conducted on the 200 attenuation values obtained from the Monte Carlo simulations to calculate their mean and standard deviation. Fig. 9 shows the mean of the attenuation results for multiple trials under different variability parameters.

Fig. 9

The impact of coefficient of variation and correlation length on the attenuation of compressional waves

From Fig. 9, when the variability parameters are elastic modulus and porosity, the mean wave attenuation increases with the increase of the correlation length and decreases with the increase of the coefficient of variation. This is because an increase in the correlation length implies an increase in the homogeneity of the medium, reducing the obstacles in the wave propagation path and thus decreasing wave attenuation, leading to an increase in the ratio. Conversely, an increase in the coefficient of variation implies an increase in the randomness of the medium, increasing wave scattering and the obstacles in the wave propagation path, thus increasing wave attenuation and decreasing the ratio. For heterogeneous soil with porosity as the variability parameter, an increase in the coefficient of variation means more frequent occurrence of high-porosity regions, which have greater resistance, leading to increased attenuation and a decrease in the attenuation ratio. Fig. 9(b) shows the variation of attenuation with correlation length and coefficient of variation when Poisson’s ratio is the variability parameter. The attenuation fluctuates very little, consistent with the above conclusion that the variability of Poisson’s ratio has a minimal impact.

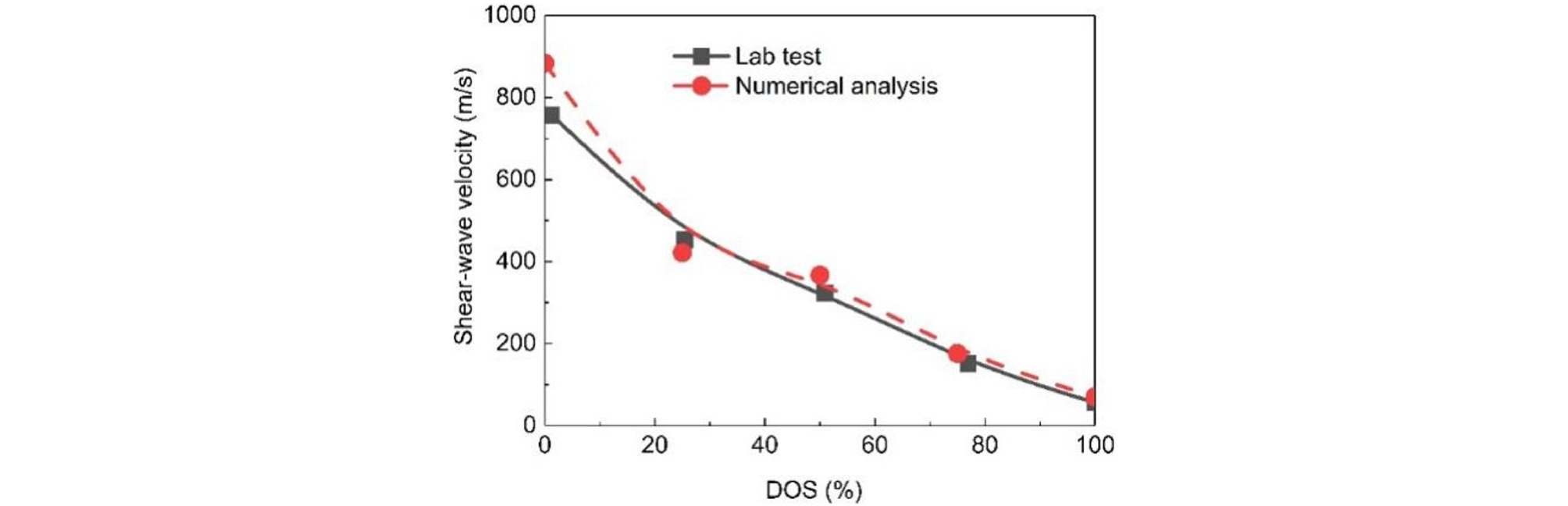
Choi et al. (2004) selected three samples—clay, weathered granite residual soil, and Jinjiang natural sand—from the Busan area in South Korea. They conducted continuous drying tests on these samples using an experimental tank setup, obtaining the shear wave velocity and resistivity of each sample at different degrees of saturation (DOS). In this study, clay was selected as the homogeneous soil for numerical simulation to obtain the shear wave velocity at different degrees of saturation, and a comparative analysis was conducted with Choi et al.’s experimental data (Fig. 10).

Fig. 10

Comparison of laboratory and numerical analysis results for shear wave velocity

The property parameters of the clay used in this article are based on the clay in Busan, South Korea selected by Choi et al. The specific property parameters are shown in the following table.

From Fig. 10, it can be seen that the shear wave velocity in clay varies with the degree of saturation (DOS), showing a high degree of fit with the laboratory experimental results. This also verifies the reliability of the numerical analysis.

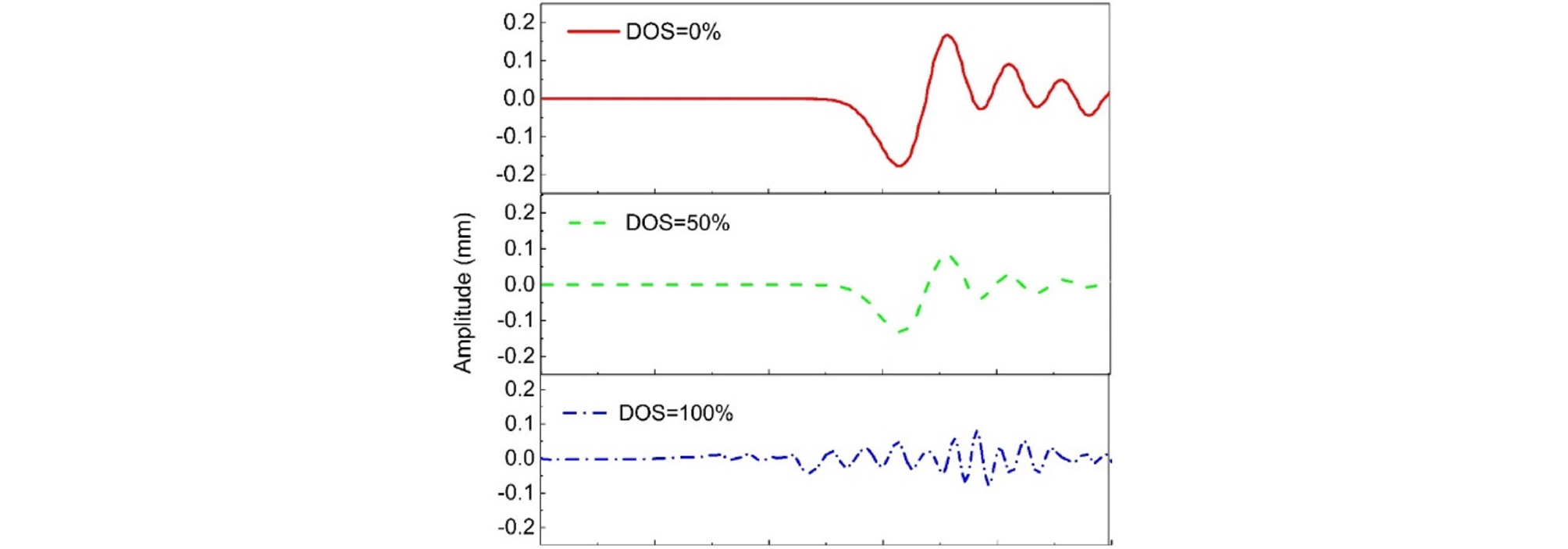
The FLAC 2D finite difference software was used to obtain the amplitude variations at different saturation levels (with the elastic modulus as the variable parameter, a coefficient of variation of 30%, and a correlation length of 0.1 m), as shown in Fig. 11. From Fig. 11, it is evident that as soil saturation increases, the amplitude of the compressional wave gradually decreases. This trend indicates that the increase in moisture content within the soil has a significant damping effect on wave propagation.

Fig. 11

Effect of saturation on amplitude variation of compression Waves in heterogeneous soil

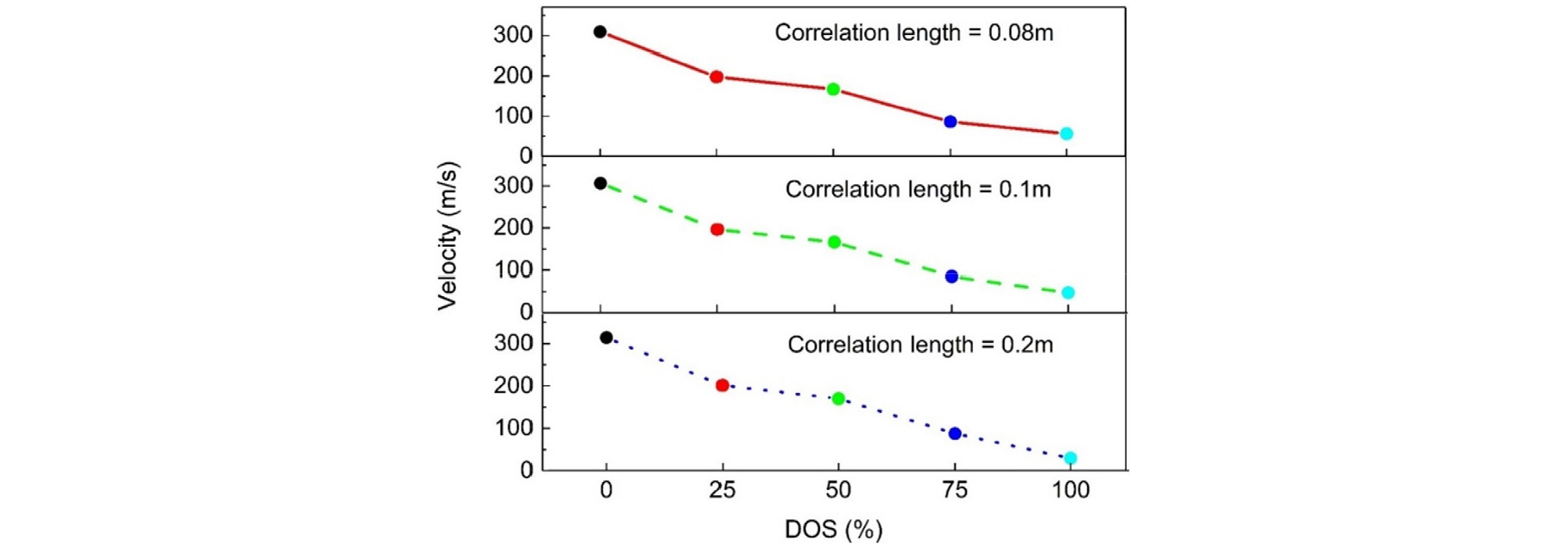
The study of the impact of soil degree of saturation on wave propagation in heterogeneous soils aims to reveal the mechanisms by which the physical and mechanical properties of soil under complex geological conditions affect the propagation characteristics of elastic waves. In summary, the variability of elastic modulus has a significant impact on wave propagation, as wave propagation characteristics are more sensitive to changes in the elastic modulus, while the variability of Poisson’s ratio and porosity has a smaller effect. Therefore, when analyzing the changes in wave velocity and attenuation with different correlation lengths and coefficients of variation, the elastic modulus was selected as the variability parameter (with a coefficient of variation of 30%). The study analyzed the changes in wave velocity and attenuation as the degree of saturation (DOS) varied from 0% to 100%, with correlation lengths of 0.08 m, 0.1 m, and 0.2 m (Figs. 12-13).

Fig. 12

Wave velocity attenuation with degree of saturation at different correlation lengths

Fig. 13

The effect of degree of saturation on attenuation at different correlation lengths

From Fig. 12, the compressional wave velocity decreases as the degree of saturation (DOS) increases. As the degree of saturation increases, the pores become filled with water, whose elastic modulus is relatively low, leading to a decrease in wave velocity. The correlation length has a relatively small impact on the change in wave velocity.

The observed trend of decreasing compressional wave velocity with increasing saturation in this study shows a certain similarity to the empirical results of Karakul and Ulusay (2013). Although their results indicate that compressional wave velocity can both decrease and increase with increasing saturation, the decrease under specific conditions aligns with our findings. This study focuses on clay, where a decrease in P-wave velocity with increasing saturation has been verified. This phenomenon can be attributed to the replacement of air in the pores by water as saturation increases, which reduces the overall rigidity of the medium. For clay, at high saturation levels, the presence of water not only reduces the compressional wave velocity but also enhances energy loss and attenuation effects. Despite the differences in research subjects, this similar trend provides reasonable support for our conclusions regarding the impact of saturation on wave velocity.

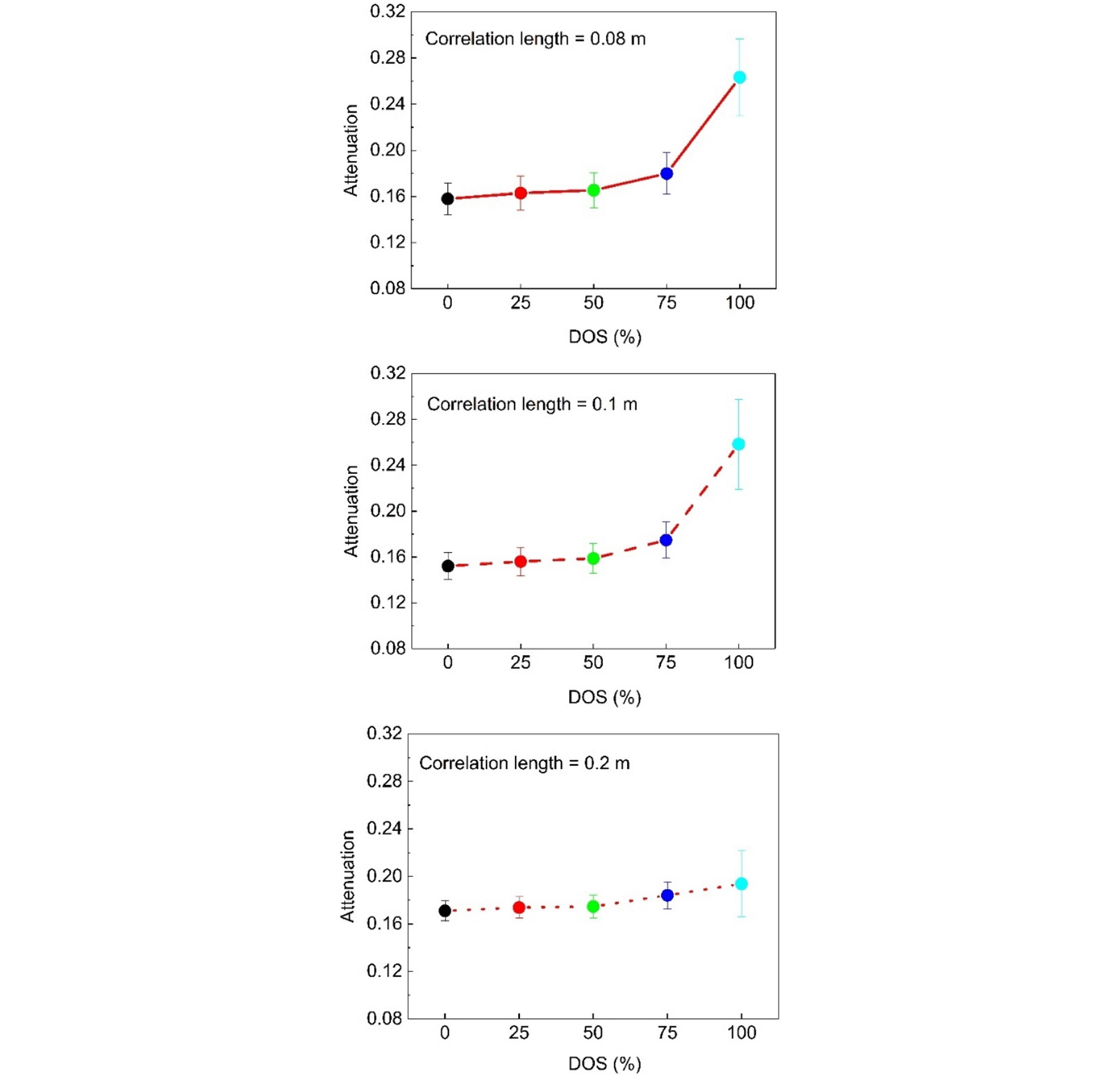
Fig. 13 shows the relationship between attenuation and the degree of saturation (DOS) under different correlation lengths in heterogeneous soil. As seen in Fig. 12, wave velocity decreases with increasing degree of saturation. Lower wave velocity results in longer wave propagation time, thereby increasing energy loss during wave propagation. Additionally, as the degree of saturation increases, the effective stress in the soil decreases, weakening the contact forces between particles. This increases the heterogeneity of wave propagation, causing more wave energy to be reflected and scattered at the interfaces between different media, thereby increasing attenuation. Finally, with increasing degree of saturation, the amount of water in the pores increases, leading to higher pore pressure. High pore pressure hinders wave propagation, resulting in more energy being absorbed during wave propagation.

5. Conclusion

The propagation characteristics of elastic waves in heterogeneous soils are crucial for geotechnical and civil engineering. The study investigated the propagation characteristics of elastic waves in heterogeneous soils, focusing on the variability in elastic modulus, Poisson’s ratio, and porosity. Using a Gaussian random field model and Monte Carlo simulations, the effects of different variability coefficients and correlation lengths on wave velocity, peak amplitude, and attenuation were analyzed.

(1) Variability in the elastic modulus significantly influences wave propagation time and peak amplitude. For instance, when the coefficient of variation increased from 10% to 30%, the peak amplitude decreased by approximately 25%, indicating a direct impact of increased heterogeneity on wave energy dissipation. The increase in the coefficient of variation complicates the wave propagation path, leading to intensified energy scattering and reflection, as observed by a 15% increase in wave arrival time at point M3. On the other hand, increasing the correlation length from 0.05 m to 0.2 m reduced the rate of amplitude reduction by nearly 18%, showing that larger correlation lengths smooth out local variations, resulting in more continuous wave propagation paths. These ratios highlight how different levels of variability affect wave propagation in heterogeneous soils, offering valuable insights for engineering applications.

(2) As soil degree of saturation increases, the amount of water in the pores rises, leading to a decrease in wave velocity. The correlation length has a minor effect on wave velocity changes. The variability parameters significantly impact wave velocity, with the variability in elastic modulus having the most substantial effect. Changes in correlation length and variability coefficient affect the complexity of the wave propagation path. Larger correlation lengths smooth the soil property variations, reducing scattering and reflection effects, while increased variability coefficients complicate the wave propagation path, resulting in more energy loss.

(3) The attenuation characteristics of waves are significantly influenced by variability parameters and soil degree of saturation. Variability in elastic modulus and correlation length markedly increases wave attenuation. Increased degree of saturation leads to longer wave propagation times and greater energy loss. Additionally, reduced effective stress and weakened inter-particle contact forces increase the heterogeneity of wave propagation, causing more energy to be reflected and scattered at different media interfaces, further increasing attenuation.

This study provides valuable insights into the propagation characteristics of waves in heterogeneous soils, revealing how soil variability and saturation influence wave velocity and energy attenuation. These findings offer theoretical support for seismic design of underground structures and groundwater flow analysis, aiding in the optimization of engineering designs and enhancing structural safety and stability. Additionally, the results provide a scientific basis for addressing geological risks associated with climate change, contributing to the development of more effective environmental remediation and sustainable engineering strategies. Moreover, this research deepens the understanding of complex soil properties, facilitating more accurate predictions and decision-making in underground engineering, thereby reducing project risks and resource consumption.