1. 서 론
2. 연구 방법
2.1 가뭄지수
2.2 포화증발산량 산정식
2.3 상관계수
3. 대상 지점의 선정 및 자료 수집
3.1 대상 기상청 ASOS 관측소
4. 가뭄지수 산정결과
4.1 SPI 산정결과
4.2 Thornthwaite 식과 Penman-Monteith 식을 이용한 SPEI 산정결과
5. 가뭄심도 분석결과
5.1 SPI 산정결과를 이용한 가뭄심도
5.2 Thornthwaite 식과 Penman-Monteith 식을 이용한 SPEI 산정결과를 이용한 가뭄심도
6. 가뭄지수 상관관계 분석
7. 결 론
1. 서 론
가뭄재해는 하천재해나 내수재해 등과 같은 풍수해에 비해 발생빈도는 현저히 작다. 가뭄의 특성상 다른 재해에 비해 가뭄은 서서히 진행되고 그 발생시점을 명확히 인지하기 어렵기 때문에 그에 따른 가뭄지속기간 등을 명확히 정의하기 쉽지 않다. 우리나라의 경우, 5 mm 이하의 일강수량 일수가 15일 이상 지속되고 1개월 강수량이 50 mm 이하인 조건을 만족하고 강수량의 차이가 없더라도 물의 증발산량이 많아서 물공급이 어려운 상황도 가뭄으로 분류하고 있다. 따라서 일반적으로 가뭄은 장기간에 걸친 강수량 부족으로 인해 발생된 가용수자원 부족으로 정의한다(Kim et al., 2013; Kim et al., 2020). 가뭄은 다양한 정의에 따라 기상학적 가뭄(meteorolgical drought), 수문학적 가뭄(hydrological drought), 농업적 가뭄(agricultural drought) 그리고 사회경제적 가뭄(socioeconomic drought)으로 분류할 수 있다(Wilhite & Glantz, 1985; Kim & Shin, 2018). 정량적인 가뭄을 명확히 평가하기 위하여 다양한 가뭄지수가 제안되었다. 본 연구에서는 물 수요에 대한 물 공급 부족에 의해 발생한다고 가정하고 있는 기상학적 가뭄에 대해 연구하였다. 따라서 기상학적 가뭄은 특정한 기간 동안 강수량을 반영하여 특정 기간 동안 합산된 강수량이 평균강수량(평년치 강수량)보다 큰지 작은지를 계량화하여 정의할 수 있다(McKee et al., 1993; Kim & Shin, 2018). 대표적인 기상학적 가뭄을 평가하기 위한 지표는 SPI(Standardized Precipitation Index, 표준강수량지수) 지표로써 일정한 시간간격에 따라 강수량의 합이 평균강수량과의 차이를 비교하여 계량화한 지표이다(McKee et al., 1993; Svoboda et al., 2012; Stagge et al., 2015). 하지만 SPI 지표의 가장 큰 단점은 물의 순환 관점에서 손실강수량에 대한 고려가 없다는 점이다. 따라서 SPI 지표를 보완하기 위하여 강수량 자료와는 별도로 수문학적 접근법에 따라 손실량 중 증발산량을 도입하여 SPEI(Standardized Precipitation Evapotranspiration Index, 표준강수증발산지수) 지표를 제안하였다(Vicente-Serrano et al., 2010; Stagge et al., 2015). SPEI 지표의 경우, 강수의 손실량을 산정하기 위하여 증발산량을 추정한다. 대표적으로 SPEI 지표에서 사용되는 증발산량 추정식은 Thornthwaite식(Thornthwaite, 1948; Shuttleworth, 1993)과 Penman-Monteith 식(Allen et al., 1998; Pereira et al., 2012)을 활용하고 있다.
본 연구에서는 대표적인 기상학적 가뭄지수인 SPI 지수를 검토하고 기상학적 가뭄지수에 수문학 요소인 증발산량을 추정하여 실제 수문학적 영향까지 고려한 가뭄지수인 SPEI 지수를 상호 검토하고자 하였다. 따라서 본 연구의 목적은 가뭄을 수문학적 측면에서 명확히 정의하고 정량화하기 위하여 물의 순환의 대표적 요소 중에서 강수량과 가장 큰 손실량을 차지하는 증발산량을 고려한 가뭄지수간의 상관관계를 분석하고자 하였다. 국내의 기상청 기상자료개방포털(Korea Meteorological Administration)에서 제공되는 종관기상관측(Automated Synoptic Observing System; ASOS)의 경우에도 복사량 및 풍속과 같은 고품질 자료의 관측이 부재하거나 관측기간이 짧은 경우, Penman-Monteith 식을 적용하여 물리적인 증발산량을 정확히 추정하기에는 어려움이 있다. 따라서, 증발산량 산정식 중에서 Thornthwaite식은 월평균기온만으로 가장 간단히 증발산량을 추정할 수 있다. 반면 복사량 또는 일사량 자료와 같은 정밀도 높은 기상관측자료 수집과 활용이 가능하다면 Penman-Monteith식을 적용해 볼 수 있다. 따라서, 본 연구에서는 Pearson 상관계수와 Spearman 순위 상관계수를 이용하여 SPI 지표와 SPEI 지표(SPEI_Thornthwaite과 SPEI_Penman-Monteith)의 가뭄기간별 가뭄지표간 상관관계 분석을 통해 적정성을 평가하였다(De Winter et al., 2016). 증발산량 산정을 위한 Penman-Monteith 식의 대안으로 Thornthwaite식을 활용할 수 있었다. 마지막으로 본 연구를 통해 제안된 SPI 지표와 SPEI 지표를 통해 강우와 증발산량에 따른 가뭄발생기간을 예측하여 국가산업단지의 공업용수 확보를 위한 선제적인 가뭄대응을 통해 안정적인 공업용수공급이 가능하리라 판단된다.
2. 연구 방법
2.1 가뭄지수
2.1.1 표준강수가뭄지수(Standardized Precipitation Index; SPI)
표준강수가뭄지수(SPI)는 특정기간 동안 발생한 강수량을 통계적으로 분석하여 해당 지역의 평균강우량과의 차이를 표준화하여 가뭄상태를 평가는 지표이다. 강수량 자료에 대해 통계적 기법을 사용하여 정규분포를 활용하는 방법이다(McKee et al., 1993; Svoboda et al., 2012; Stagge et al., 2015).
SPI는 수집된 강수량 자료에 대해 감마 분포(Gamma Distribution)의 누적확률분포로 변환하여 통계분석을 실시한다.
여기서, = 강수량, = 감마분포의 모수, = 감마분포의 척도모수, = 감마함수. 단, 무강수량인 경우, 0 강수량을 분리하고 감마분포를 적용해야 한 후, 0 강수량의 확률을 더해야 한다. 강수량을 정규분포로 변환하기 위해 누가확률이 일때의 정규분포의 표준화된 누가확률을 갖는 값으로 변환하여 SPI를 산정한다.
여기서, = 누적확률 에 대한 표준정규분포의 역함수이다. 따라서, SPI 지표는 강수량을 감마분포로 통계분석한 후, 정규분포로 변환하여 표준화된 값을 산출하여 평균 0과 표준편차 1의 값으로 가뭄의 상태를 정량화한 지수이다. 단, SPI 지표와 SPEI 지표 모두 동일한 가뭄분규 체계를 사용하고 음수는 가뭄을 양수는 습윤상태를 나타낸다(Table 1). 본 연구에서 사용된 SPI와 SPEI의 가뭄지표에 사용된 가뭄심도는 분류체계는 slight drought(경미한 가뭄), moderate drought(약한 가뭄), severe drought(심한 가뭄), extreme drought(극심한 가뭄)으로 총 4개 단계로 분류할 수 있다(Kim et al., 2020; Zhang et al., 2019).
Table 1.
Drought classification criteria by drought index (SPI and SPEI) (Kim et al., 2020; Zhang et al., 2019)
2.1.2 표준강수증발산가뭄지수(Standardized Precipitation Evapotranspiration Index; SPEI)
표준강수증발산가뭄지수(SPEI)는 SPI와 동일한 통계기법으로 계산되지만 강수량뿐만 아니라 증발산량(Evapotranspiration; PET)까지 함께 고려하여 가뭄상태를 평가하는 지표이다(Vicente-Serrano et al., 2010; Stagge et al., 2015). 증발산량까지 고려하기 때문에 증발산량 산정식에 따라 기온을 포함한 다양한 기상 자료를 이용하게 된다. 즉, SPEI는 물의 공급량인 강수량과 기온변동량이 반영된 수요량인 증발산량이 고려된 수문학적 물수지분석을 활용한 평가 지표이다.
여기서, = 물수지(water Deficit), = 강수량, = 잠재증발산량이다.
SPI와 동일하게 SPEI도 물수지에 대해 감마 분포를 적용한 후, 표준정규분포로 변환하여 SPEI 지표를 산출하였다. Table 1에서 언급한 바와 같이 SPEI 지표도 동일한 가뭄 분류체계를 사용하였다.
SPEI는 SPI과 다르게 잠재증발산량을 산정해야 하기 때문에 다양한 증발산량 산정식을 활용할 수 있다. 대표적으로 Thornthwaite 방법(Thornthwaite, 1948; Shuttleworth, 1993)이나 Penman-Monteith 방법(Allen et al., 1998; Pereira et al., 2012)을 활용하여 잠재증발산량을 산정한 후, 강수량의 차이를 구하여 물수지 계산을 수행할 수 있다. 본 연구에서도 이 2가지 대표적인 잠재증발산량 산정 방법을 활용하여 SPI와 SPEI 지표를 산정하여 분석하였다.
2.1.3 SPI와 SPEI 지표 비교
SPI 지표와 SPEI 지표의 중요한 차이는 Table 2에서 보는 바와 같다. 앞서 언급한 바와 같이 SPEI 지표는 SPI 지표와는 다르게 잠재증발산량을 고려하기 때문에 기후변화 및 간단한 물수지분석을 통한 정밀한 가뭄 평가가 가능하다. 하지만 강수량 자료 뿐만 아니라 증발산량 산정식에 따라 기온 자료를 포함하여 정밀한 추가 기상자료가 필요하기 때문에 고품질 기상자료의 확보가 어려운 지역에서 적용하기에는 제한적이다.
Table 2.
Comparion of SPI and SPEI
2.2 포화증발산량 산정식
2.2.1 Thornthwaite 방법
Thornthwaite 방법은 월평균기온 자료만으로도 증발산량을 추정할 수 있는 매우 간단한 경험적 모형이다(Thornthwaite, 1948; Shuttleworth, 1993).
여기서, = 일증발산량(mm/day), = 월평균 기온(℃), = 연 온도지수, = 경험계수,
Thornthwaite 방법은 기온자료만으로 증발산량을 효과적으로 계산할 수 있는 매우 간단한 경험식이다. 따라서, 기상자료 수집이 어려운 지역에서도 널리 사용할 수 있다. 다만, 기온만을 고려하기 때문에 정확도가 낮으며, 다른 기상요소인 풍속, 습도, 복사량 등을 반영하지 못하는 한계가 있다.
2.2.2 Penman-Monteith 방법
Penman-Monteith 방법은 토양 자료와 기상 자료를 활용하여 증발산량(Evapotranspiration; ET)을 추정하는 물리기반 모형이다(Allen et al., 1998; Pereira et al., 2012).
여기서, = 일증발산량(mm/day), = 순복사량(MJ/m2/day), = 토양열 플럭스(MJ/m2/day), = 일평균기온(℃), = 2 m 높이에서의 풍속(m/s), = 포화 수증기압(kPa), = 실제 수증기압(kPa), = 기온변화에 따른 포화 수증기압 변화율(kPa/℃), = 비열비(kPa/℃).
Penman-Monteith 방법은 다양한 기상현상을 고려하여 정확한 증발산량을 산정할 수 있다. 기상 자료의 활용이 충분히 가능하다면 여러 기상 조건 하에서도 정확한 증발산량 예측이 가능하며, 지역별 기상관측소의 관측값을 기반으로 효과적인 증발산량을 산정할 수 있는 방법이다(Allen et al., 1998; Korea Meteorological Administration, 2016). Eq. (7)의 상세한 계산과정은 다음과 같다: ① 2 m 풍속 계산, ② 건습계 상수 계산, ③ 포화수중기압 계산식(kPa), ④ 기온에 따른 포화수중기압의 기울기 계산, ⑤ 총 복사량 계산, ⑥ 토양 열속 밀도 계산, ⑦ 증발산량 계산. 단점으로는 복사량이나 풍속과 같은 고품질 기상자료가 확보되지 않는다면 계산에 어려움이 있고 다양한 기상변수를 고려해야 하기 때문에 자료의 수집과 계산이 복잡하다.
2.3 상관계수
2.3.1 Pearson 상관계수(Pearson’s Correlation Coefficient)
Pearson 상관계수 은 3개 변수 사이의 선형 관계를 측정하는 방법이다(De Winter et al., 2016).
여기서, = 각 변수값, = 각 변수의 평균값, = 자료의 개수.
Pearson 상관계수는 계산이 직관적이며, 변수간의 선형관계를 명확히 파악할 수 있다. 또한 2개의 변수간의 선형 관계가 있고 정규분포를 따를 때 적합하게 사용할 수 있다. 하지만 Spearman 상관계수와는 다르게 이상치(outliers)에 대해 매우 민감하며, 상관계수가 왜곡될 수 있는 단점이 있다. 따라서, 자료가 비정규분포를 따를 때 신뢰도는 크게 떨어진다.
2.3.2 Spearman 순위 상관계수(Spearman’s Rank Correlation Coefficient)
Spearman 상관계수 는 2개의 변수간 단조(monotonic) 관계를 분석하기 위하여 자료의 순위기반 상관관계를 분석하는 방법이다(De Winter et al., 2016).
여기서, = 각 자료의 순위차, = 자료의 개수.
Spearman 상관계수의 경우, 변수간의 비선형 단조(monotonic) 관계에 대한 상관관계를 측정할 수 있다. 자료의 순위를 고려하기 때문에 자료가 정규분포로 가정하지 않아도 되며, 이상치 처리에도 적절히 계산되는 장점이 있다. 다만, 자료가 순위기반으로 분석하기 때문에 자료의 절대적 크기를 무시하고 동일한 순위를 가진 변수간의 처리에서는 어려움이 발생한다.
3. 대상 지점의 선정 및 자료 수집
3.1 대상 기상청 ASOS 관측소
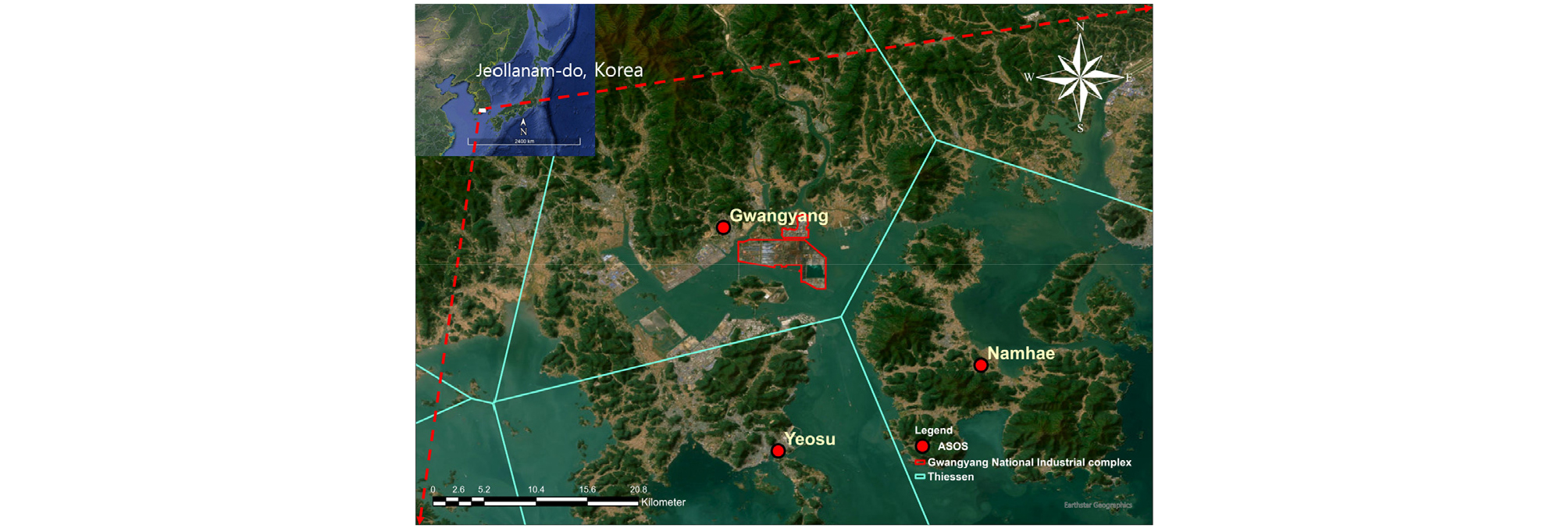
가뭄지수 평가를 위해서 사용된 강수량 자료 및 기상자료는 기상청 기상자료개방포털(Korea Meteorological Administration, www.data.kma.go.kr)에서 제공되는 종관기상관측(ASOS) 자료를 사용하였다. 본 연구에서 사용된 기상청 기상관측소의 위치는 Fig. 1에서 보는 바와 같이 광양국가산업단지 인근에 위치하고 있다. 따라서, 인근 지역의 용수공급을 포함한 전체 물공급 평가를 위한 가뭄평가는 선행되어야 한다.
광양ASOS기상관측소는 기상청 광주지방기상청 관측과에서 운영하고 있으며, 전라남도 광양시 중동 산109-3에 위치하고 있다(Fig. 1). 기상청 Open-API를 활용하여 강수량 자료 및 기상자료를 수집하기 위해서는 Table 3의 ASOS 관측소 정보가 필요하다. Table 3에서 보는 바와 같이 광양관측소의 경우, 타 ASOS 기상관측소와는 다르게 관측개시일이 비교적 짧은 2011년 4월 5일부터 기상 및 수문자료를 관측하기 시작했다. 하지만 증발산량 산정을 위해 Penman-Monteith 방법을 사용할 경우, 일순복사량(일사량) 자료가 반드시 필요하다. 하지만 타 ASOS 기상관측소의 경우, 일순복사량 자료가 없거나 상대적으로 더 짧은 일부 자료만이 축적되었기 때문에 광양기상관측소의 전체 기상자료에 대한 관측기간이 짧음에도 불구하고 본 연구의 목적에 부합하기에 광양기상관측소를 선정하였다.
Table 3.
Gwangyang ASOS meteorological observatory
| Station | Station No. | WGS84 coordinate system |
Elevation (EL.m) |
Date of commencement of observation | |
| Latitude | Longitude | ||||
| Gwang-yang | 266 | 34.943 | 127.691 | 88.21 | 2011-04-05 |
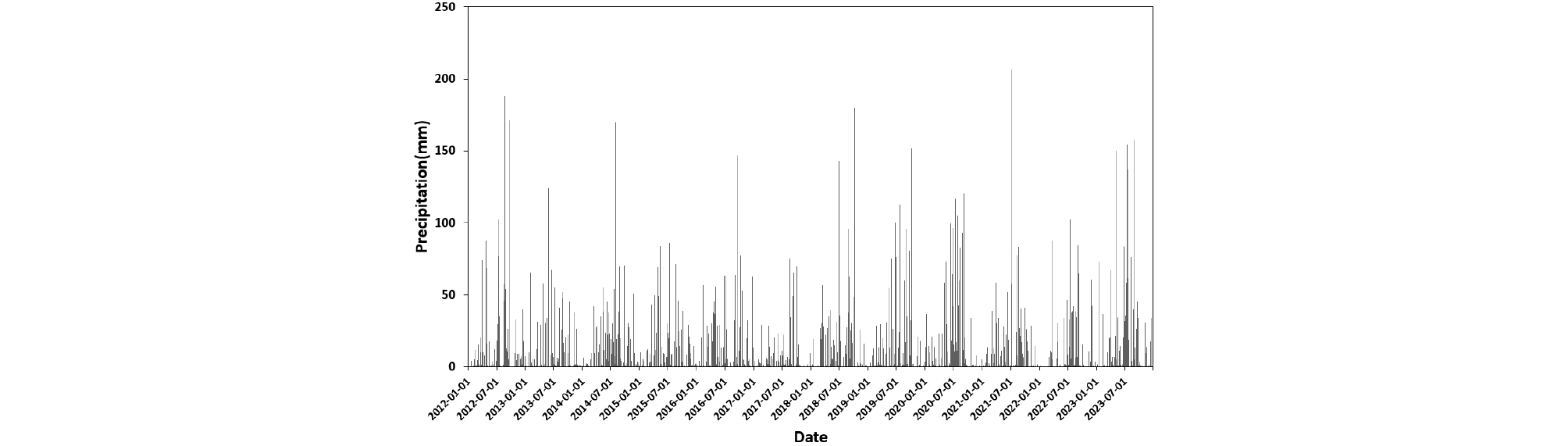
본 연구에서는 수문 및 기상자료를 활용한 SPI 및 SPEI 기상학적 가뭄 분석을 위하여 가뭄기간을 1개월, 3개월, 6개월, 9개월, 12개월, 18개월, 24개월로 설정하여 단기 가뭄부터 장기 가뭄 발생에 대해서 검토하였다. SPI 및 SPEI 분석을 위해 Fig. 2에서 보는 바와 같이 광양기상관측소에서 수집된 2012년 1월 1일~2023년 12월 31일까지 총 12년 강수량 시계열 자료를 활용하였다.
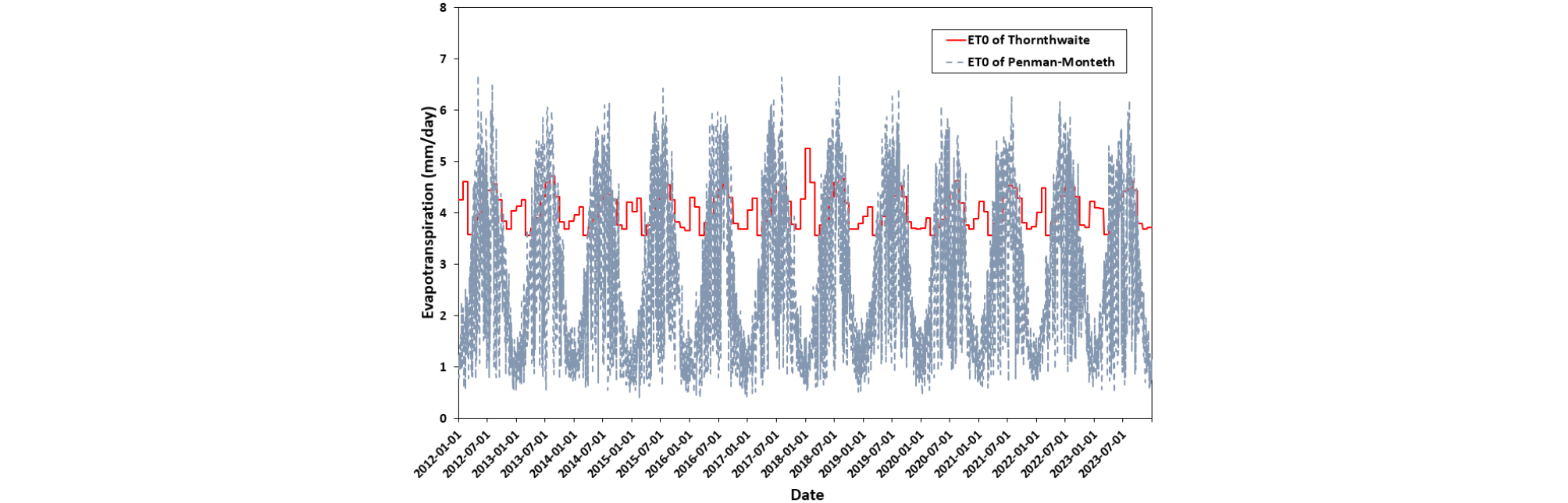
수집된 기상자료인 습도, 풍속, 복사량 등을 활용하여 Fig. 3에서와 같이 증발산량을 계산하였다. 증발산량 산정을 위해 Thornthwaite식과 Penman-Monteith 식을 활용하였다. Thornthwaite식으로 계산된 증발산량은 월평균기온 기반의 경험적 모형이기 때문에 기온, 습도, 풍속, 복사량 등 기상 인자를 고려한 물리기반 모형인 Penman-Monteith 식에 비해 계절변화에 따른 기상현상을 상세히 반영하지 못하고 있다. Fig. 3에서 보는 바와 같이 겨울철의 경우, Thornthwaite식으로 산정된 증발산량은 Penman-Monteith 식에 의해 계산한 증발산량에 비해 과대추정되고 있으며, 반대로 여름철의 경우, Thornthwaite 식의 증발산량은 Thornthwaite 식의 증발산량에 비해 과소추정되고 있다. 따라서, Thornthwaite 식에 의한 증발산량은 3.56~5.25 mm/day 범위에서 일정한 변동폭을 보이고 있다. 이는 계절변화에 따른 습도, 풍속 등의 변화를 제대로 반영하지 못하고 월평균기온만을 반영하여 개략적으로 증발산량을 추정했기 때문이라고 판단된다. 반면 Penman-Monteith 식에 의해 계산한 증발산량은 0.39~6.68 mm/day는 계절적 변동을 잘 반영하고 있다.
4. 가뭄지수 산정결과
4.1 SPI 산정결과
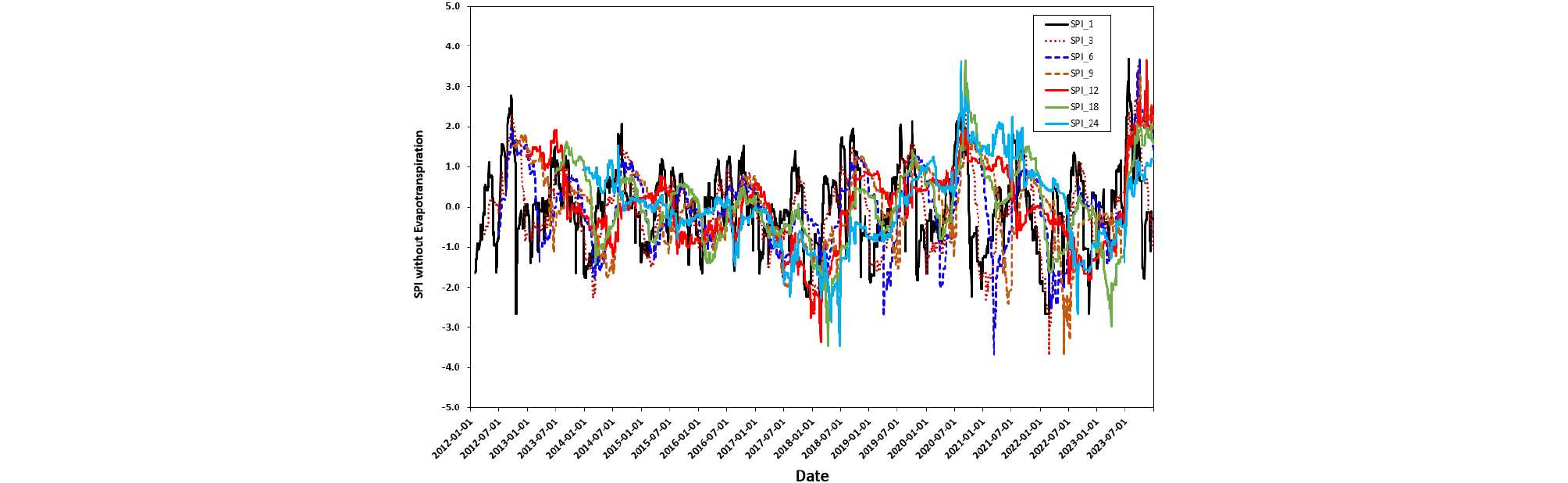
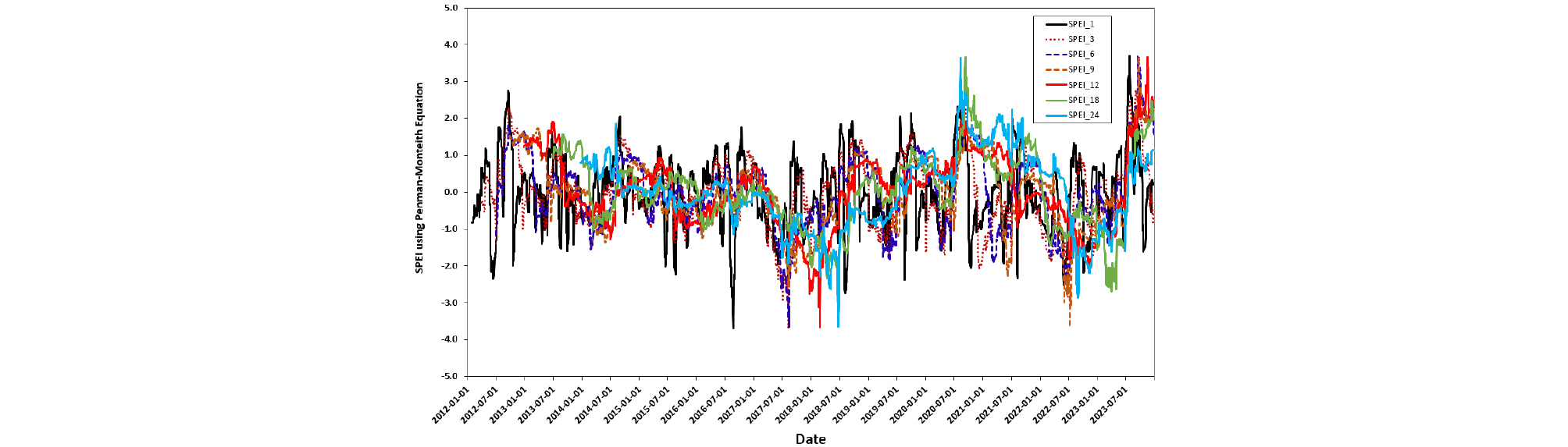
Fig. 4는 기온이나 증발산량을 반영하지 않는 강수량 자료만을 활용하여 도출한 SPI 지표 결과이다. Table 1에서 제시하고 있는 지표에 근거하여 Fig. 4에서 보는 바와 같이 SPI 가 2 이상의 극심한 습윤상태에 대한 빈도는 계절변동에 따라 기온 및 증발산량을 고려한 Fig. 6의 SPEI 결과보다 더 큰 빈도로 발생하고 있다. 반면, -2 이하 극심한 가뭄 발생의 경우에는 SPI에 비해 오히려 SPEI가 -4 이하의 매우 극심한 가뭄이 더욱 더 빈번히 발생하고 있다. SPI 지표의 경우, 가뭄 분석을 위해 단지 강수량 자료만을 활용하였고 증발산에 의한 수분 손실량에 대한 고려가 없기 때문에 SPI는 SPEI에 비해 과소추정되었다.
Fig. 4~Fig. 6에서 보는 바와 같이 SP_1에 해당한 가뭄기간 1개월 이내의 단기 극심한 가뭄은 2018년 이전에는 빈번히 발생하고 있으며, 18개월 가뭄기간(SP_18) 및 24개월 가뭄기간(SP_24)에 대해서는 2020년 여름에는 극심한 습윤상태로 분석되었다. Fig. 4의 SPI 결과는 2017년 여름 이전까지는 1개월(SP_1) 이내의 단기 극심한 가뭄의 발생빈도는 중장기 가뭄에 비해 빈번히 발생하고 있다. 특히 2012년 가을에는 1개월 단기 극심한 가뭄(SP_1)이 발생했음을 알 수 있다. 가뭄기간 24개월(SP_24)에 해당하는 극심한 가뭄은 2018년 봄부터 2019년 겨울까지 지속되었으며, 6개월 중기 가뭄(SP_6)의 경우, 2021년 봄에 분석기간 중 가장 극심한 가뭄심도가 나타났다. 또한 3개월 단기 가뭄(SP_3)은 2022년 봄에도 역시 가장 극심한 가뭄지표를 보였으며, 9개월 중장기 가뭄(SP_9)에서도 2022년 봄에서 겨울 기간 동안 극심한 가뭄심도를 보였다.
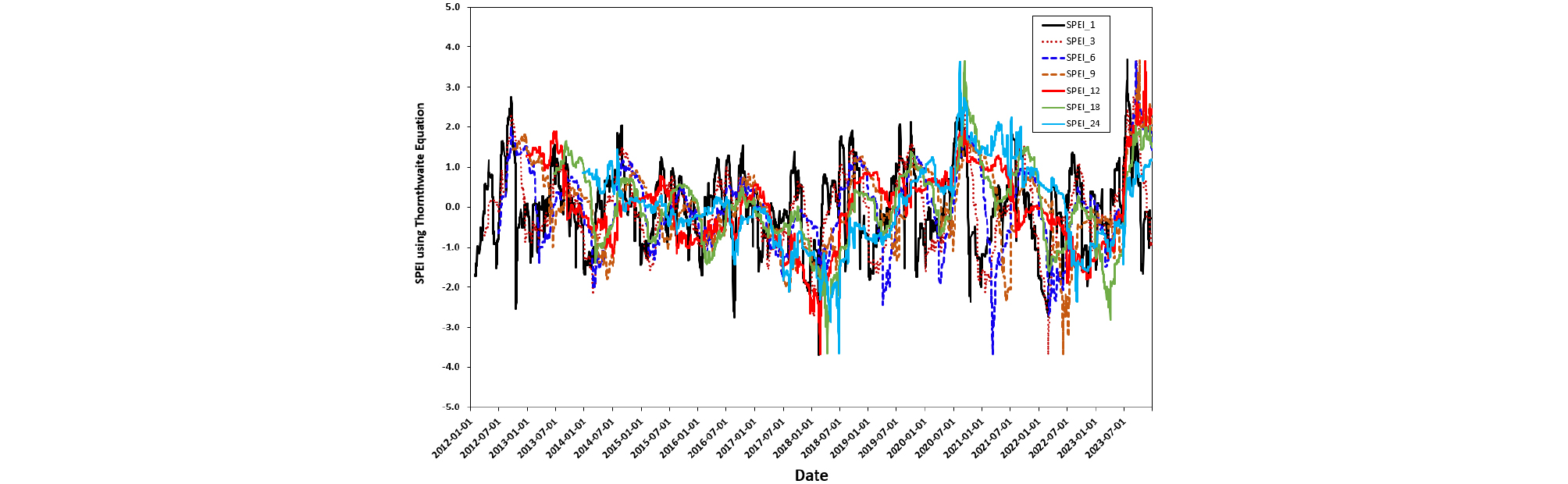
4.2 Thornthwaite 식과 Penman-Monteith 식을 이용한 SPEI 산정결과
SPI 지표와는 달리 SPEI 지표의 경우, 손실강우량을 고려한 증발산량만큼 지표면에서의 수분함유량이 감소되기 때문에 SPI에 비해 SPEI가 -2 이하의 극심한 가뭄이 1개월 단기 가뭄(SPEI_1)에서 더욱 더 빈번하게 나타나고 있다. Penman-Monteith식에 의한 가뭄심도(Fig. 6)가 Thornthwaite식에 의한 가뭄심도(Fig. 5)보다 더 극심하였다. Fig. 3에서 고찰한 바와 같이 Thornthwaite식에 의해 산정된 증발산량은 계절에 따른 차이가 작은 반면, Penman-Monteith 식에 의해 산정된 증발산량은 계절에 따른 변동량이 0.39~6.68로 매우 크기 때문에 장기 가뭄(SPEI_12, SPEI_18, SPEI_24)뿐만 아니라 1개월 가뭄(SPEI_1)의 -3.0 이하의 가뭄이 크게 발생하였다.
하지만, Fig. 6에서 Penman-Monteith 식에 의해 산정된 중기 가뭄(SPEI_6)의 경우, SPI와 같이 2021년 봄에 가장 극심한 가뭄이 일부 발생하는 것으로 계산되었다. 따라서, 2020년 여름부터 2021년 겨울까지는 12개월 이상의 SPEI_12, SPEI_18, SPEI_24의 장기 가뭄지수는 습윤상태를 유지하고 있지만 중기 가뭄지수인 SPEI_6의 경우에는 2021년 봄에 가뭄심도가 크게 계산되었다. 2023년 겨울이후에는 집중호우와 호우발생기간에 길었기 때문에 2022년 봄에 발생된 가뭄부터 2023년 봄까지 지속된 가뭄은 대부분 해소되었다고 판단된다.
5. 가뭄심도 분석결과
5.1 SPI 산정결과를 이용한 가뭄심도
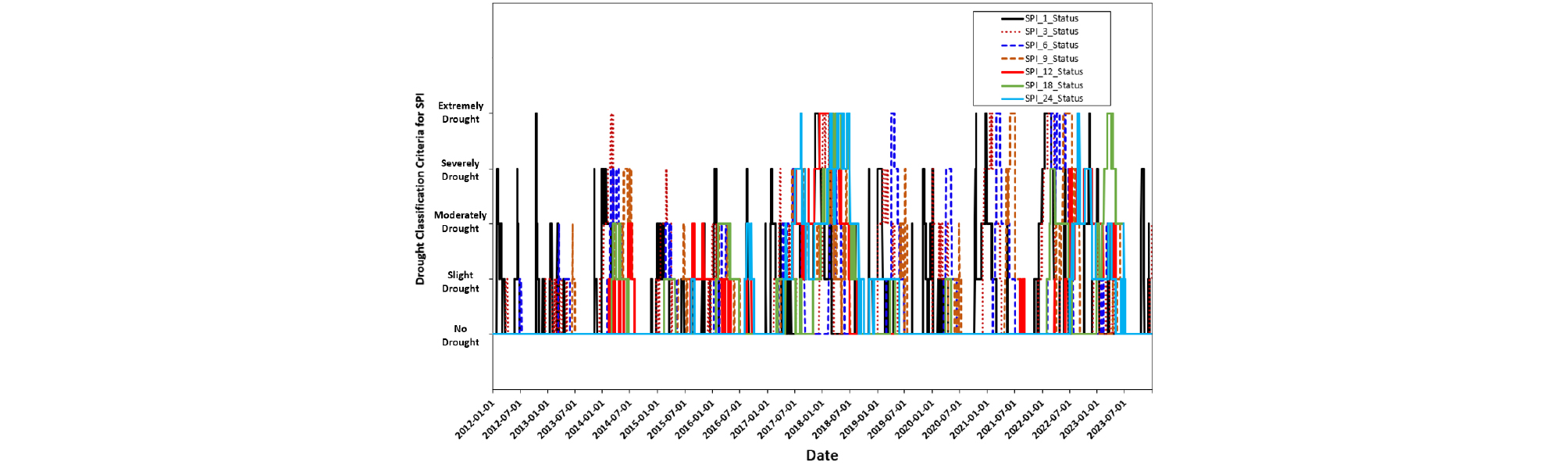
Table 4에서는 SPI를 활용하여 총 관측기간(2012년 1월 1일~2023년 12월 31일) 중에 발생한 가뭄심도별 가뭄기간(가뭄발생 일수)과 가뭄비율을 분석하였다. Fig. 7은 총 관측기간에 걸친 시계열로 발생된 가뭄심도별 가뭄기간을 도시하였다. 즉, 가뭄기간별 가뭄심도를 나타내는 척도에 따라 가뭄발생 일수과 비율을 나타내었다. SPI 지표에 따른 가뭄발생일에 대해 분석한 결과, 가뭄이 발생하지 않는 습윤상태는 전체 기간의 69.08~69.18%를 차지하고 나머지 30.92~30.82% 기간에 대해서는 경미한 가뭄부터 극심한 가뭄에 이르기까지 광범위하게 발생되는 것으로 분석되었다. 극심한 가뭄(extreme drought)의 경우, 가뭄기간에 관계없이 전 기간의 2.21~2.28%로 자주 발생하지 않는 것으로 평가되었다. 극심한 가뭄에서 상대적으로 약한 가뭄이 발생할 경우, 가뭄발생 일수는 점차 증가함을 알 수 있다. 따라서, 광양기상관측소에 위치한 국가산업단지에 공급되는 공업용수에 영향을 끼치는 가뭄심도는 통상 극심한 가뭄이 발생했을 때, 공업용수 공급 등에 대한 사전대책 마련과 주의가 필요할 것으로 판단된다.
Table 4.
The ratio of drought occurrence to total observation by SPI
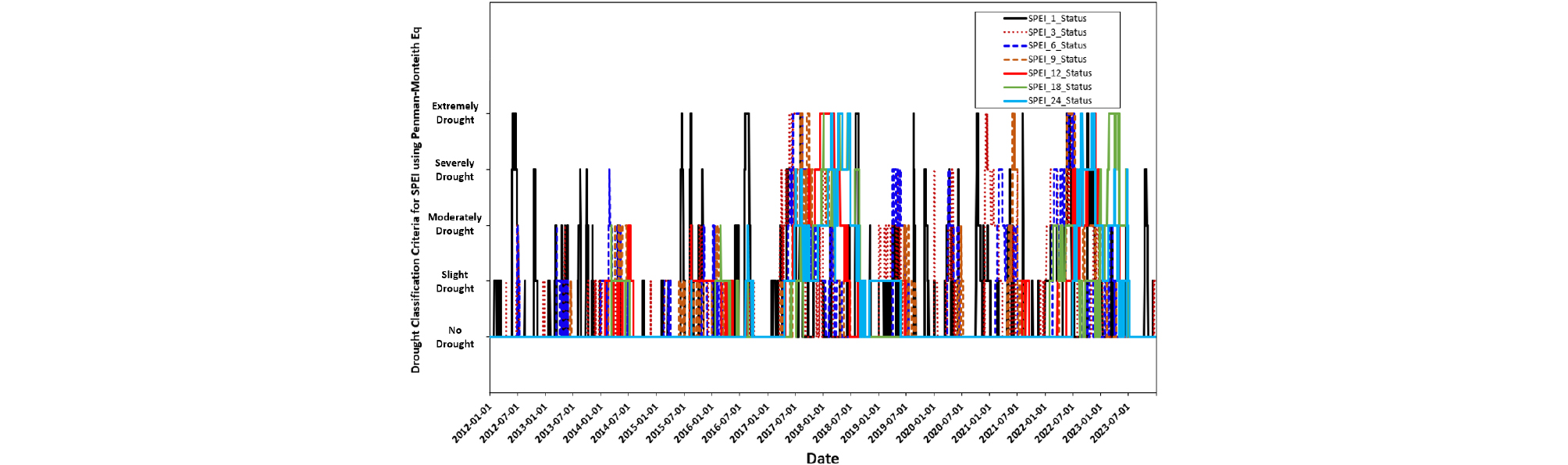
5.2 Thornthwaite 식과 Penman-Monteith 식을 이용한 SPEI 산정결과를 이용한 가뭄심도
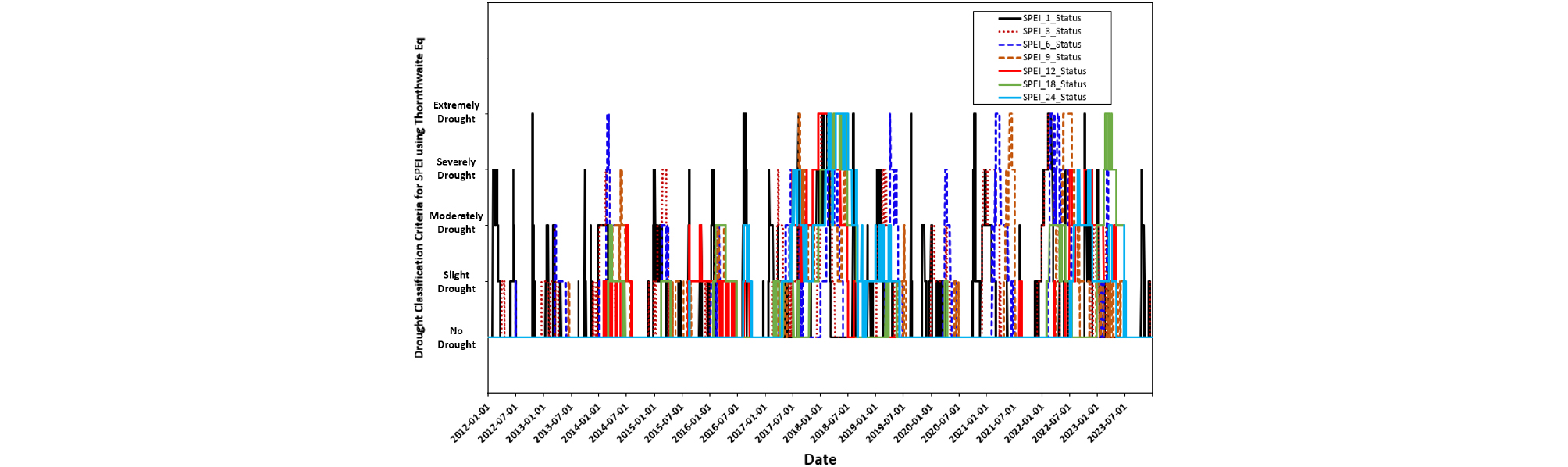
Table 5와 Table 6은 SPEI를 활용하여 앞선 SPI와 동일한 절차에 따라 총 관측기간 중에 발생한 가뭄심도별 가뭄기간과 가뭄비율을 분석하였다. SPEI 지표의 경우, Thornthwaite식과 Penman-Monteith 식을 이용한 방법에 의해 물공급 손실량을 고려한 증발산량만큼 물공급량이 줄어들기 때문에 앞서 분석된 SPI 지표에 비해 가뭄심도에 따른 가뭄발생 일수는 다소 증가하였다. Table 5의 경우, Thormthwaite식을 이용한 SPEI 지표에서 공업용수 공급에 차질이 발생할 수 있는 극심한 가뭄발생 일수는 83~106일로 SPI 지표의 82~99일보다 다소 증가된 것으로 분석되었다. 반면 Table 6의 경우, Penman-Monteith 식을 이용한 SPEI 지표의 극심한 가뭄발생 일수는 SPI 지표와 거의 동일한 수준으로 83~99일로 분석되었다. 이는 Fig. 8과 Fig. 9의 시계열 가뭄심도를 분석한 결과, Thormthwaite식을 이용한 SPEI 지표에서는 겨울철 증발산량이 Penman-Monteith 식으로 계산된 증발량에 비해 과대추정된 결과이다. 즉, 겨울철 가뭄발생 빈도 증가는 Thornthwaite식을 이용한 SPEI 지표가 반영된 결과라고 판단된다.
Table 5.
The ratio of drought occurrence to total observation by SPIE using thornthwaite Eq.
Table 6.
The ratio of drought occurrence to total observation by SPIE using Penman-Monteith Eq.
6. 가뭄지수 상관관계 분석
가뭄지수간의 상관관계를 평가하기 위하여 동일한 기간(2012년 1월 1일~2023년 12월 31일)으로 산정된 가뭄지수간의 상관계수를 산정하였다(Tables 7~8). 본 연구에서는 SPI 지표와 2개의 SPEI 지표(SPEI_Thornthwaite 지표와 SPEI_Penman-Monteith 지표) 간의 Pearson 상관계수와 Spearman 상관계수를 이용하여, 가뭄기간별 가뭄지수간의 상관관계를 평가하였다. Pearson 상관계수와 Spearman 상관계수는 모든 가뭄지수에서 유사한 결과를 얻을 수 있었다. 다만, Spearman 상관계수의 특징은 가뭄지표가 서열척도일 때 사용하는 값으로 가뭄지표의 값이 아닌 순위만을 가지고 비교되는 가뭄지표간의 연관성을 보는 지표로써의 특징을 나타낸다고 할 수 있다. 따라서, Pearson 상관계수는 비교되는 가뭄지표가 선형관계성을 분석하는 것과 대조적으로 Spearman 상관계수는 1개의 가뭄지표가 증가할 때 나머지 다른 가뭄지표가 증가하는지 감소하는지의 관계를 분석할 수 있다. SPI 지표와 SPEI_Thornthwaite 지표 및 SPEI_Penman-Monteith 지표간의 동일한 가뭄기간에 대해 비교할 경우(Tables 7~8, Tables 9~10), Spearman 상관계수는 Pearson 상관계수를 분석했을 경우보다 다소 상관성이 크게 분석되었다. 또한 SPEI_Thornthwaite 지표가 SPEI_Penman-Monteith 지표에 비해 상관성이 크게 분석되었다(Tables 7~10).
Table 7.
Pearson’s correlation coefficient matrix using thornthwaite equation
Table 8.
Spearman’s correlation coefficient matrix using thornthwaite equation
Table 9.
Pearson’s correlation coefficient matrix using Penman-Monteith equation
Table 10.
Spearman’s correlation coefficient matrix using Penman-Monteith equation
SPI 지표 간의 상관계수는 단기 가뭄(SPI_1)과 장기 가뭄(SPI_18)사이에는 거의 서로 상관관계가 없었으며, 오히려, 중기 가뭄(SPI_9)과는 음의 상관계(-0.033과 -0.108)를 가지고 있으며, 단기 가뭄과 중기 가뭄은 오히려 상관성이 없음을 알 수 있다(Tables 7~10). 또한 동일 가뭄기간에 대한 SPI 지표와 SPEI_Thornthwaite 지표 및 SPEI_Penman-Monteith 지표간에는 큰 상관성을 나타내고 있지만 SPEI_Thornthwaite 지표보다는 SPEI_Penman-Monteith 지표가 SPI 지표와 상관성이 다소 작게 산정되었다. 그 이유는 PEI_Thornthwaite 지표의 경우, 강수량과 증발산량을 산정하여 물손실량을 계산하지만 SPEI_Penman-Monteith 지표에서 계산된 증발산량에 비해 상대적으로 계절적 변동성이 적고 물손실량이 상대적으로 작기 때문에 PEI_Thornthwaite 지표가 SPEI_Penman-Monteith 지표보다 SPI 지표와 좀 더 상관관계가 크게 분석되었다.
7. 결 론
본 연구에서는 광양 국가산업단지에 위치한 광양 ASOS 기상관측소의 가뭄지수를 산정하고 분석하였다. 가뭄재해는 가뭄의 발생 시기, 가뭄발생일, 가뭄 지속기간을 명확히 파악하기 어렵기 때문에 본 연구에서는 대표적인 기상학적 가뭄지수인 SPI와 SPEI 지표(SPEI_Thornthwaite 지표 및 SPEI_Penman-Monteith 지표)를 활용하여 가뭄발생일수를 산정하였으며, 다음과 같은 결과를 도출하였다.
(1) 가뭄지표별 가뭄발생일수 비교
가뭄지표별로 가뭄발생일을 비교한 결과 SPI 지표와 SPEI 지표는 거의 유사한 결과를 나타냈다. 다만, 증발산량을 고려한 물손실량의 크기가 SPI_Thornthwaite 지표에 비해 SPEI_Penman-Monteith 지표가 더 크게 나타나므로 가뭄발생일수는 증가하는 것으로 평가되었다.
(2) 가뭄지표별 상관관계 분석
SPEI_Penman-Monteith 지표에서 계산된 증발산량에 비해 SPEI_Thornthwaite 지표의 증발산량이 상대적으로 계절적 변동성이 작고 물손실량이 상대적으로 작기 때문에 SPEI_Thornthwaite 지표가 SPEI_Penman-Monteith 지표보다 물손실량을 고려하지 않는 SPI 지표와 상관관계가 큰 것으로 나타났다. 따라서, 산정된 가뭄지수의 평가결과에 근거하여, 물손실량을 물리적으로 고려하고 있는 SPEI_Penman-Monteith 지표가 물손실량의 고려가 전혀 없이 강수량 자료만을 활용하고 있는 SPI 지표와 증발산의 계절적 변동성이 적게 산정된 SPI_Thornthwaite 지표에 비해 매우 정성적으로 적정하게 산정되었다고 평가된다.
(3) 국내 기상청 ASOS자료 기반 가뭄지표의 적용성
대부분의 국내 기상청 ASOS관측소의 경우, 복사량(또는 일상량) 및 풍속 등과 같은 고품질 기상자료에 대한 관측이 부재하거나 자료개수가 부족하기 때문에 Penman-Monteith 식을 이용한 증발산량 추정에 어려움이 있다. 따라서, 현재 기상청에서 관측된 ASOS 자료만을 활용하여 효과적인 증발산량 추정을 위한 대안으로는 월평균기온만을 활용한 Thornthwaite 식을 사용할 수 있었다. 따라서, 실무적용성 측면에서 본 연구를 통해 도출한 결과는 SPI 지표를 사용하기 보다는 수문순환적 측면에서 SPI_Thornthwaite 지표를 사용할 경우, 좀 더 SPEI_Penman-Monteith 지표에 부합한 적용성을 가지고 있음을 확인할 수 있었다.